线性代数的本质
序言
There is hardly any theory which is more elementary than linear algebra, in spite of the fact that generations of professors and textbook writers have obscured its simplicity by preposterous calculations with matrices.
尽管一批教授和教科书作者用关于矩阵的荒谬计算掩盖了线性代数的简明性,但鲜有比之更基本的理论。
本文旨在拨开繁杂计算的迷雾,回归线性代数的几何本质。我们将一起探索核心概念背后的几何直观,理解它们为何如此运作,而不仅仅是记忆抽象的运算规则。将只停留在数值运算和公式的线性代数与可视化几何直观(Visual Geometric Intuition)结合,整理自3Blue1Brown的系列视频。内容涉及到向量,线性变换,行列式,逆矩阵,点积与叉积,特征向量与特征值等,以及二次型,相似矩阵等补充内容,并辅以生动实例和讲解。

我们为什么需要几何直观
在开始之前,想象学习一个事物(概念)的场景:我们需要学习正弦函数 \(\sin(x)\) ,非常不幸的是,你遇到的教材告诉你,正弦函数是这样的:
\[ \sin(x) = x - \frac{x^3}{3!} + \frac{x^5}{5!} + \cdots + (-1)^n\frac{x^{2n+1}}{(2n+1)!} + \cdots \]
看上去很厉害的样子,并且计算机也的确是这么计算 \(\sin(x)\) 的,而对你来说,计算 \(\sin(\frac{\pi}{6})\) 可能就是把 \(x = \frac{\pi}{6}\) 代入公式,然后神奇的发现结果越算越接近0.5 ,此时你对 \(\sin(x)\) 与三角形之间的几何直观只有一些模糊的概念,这样的学习就十分悲催了。为什么呢?再假设一个场景:
在学完 \(\sin(x)\) 函数后,你又去参加了一个物理课程,正弦函数随处可见,其他人很快就能知道如何使用它并能得出大概值,而刚学完正弦函数的你内心戏大概是这样的:这群学物理的脑子也太强了!
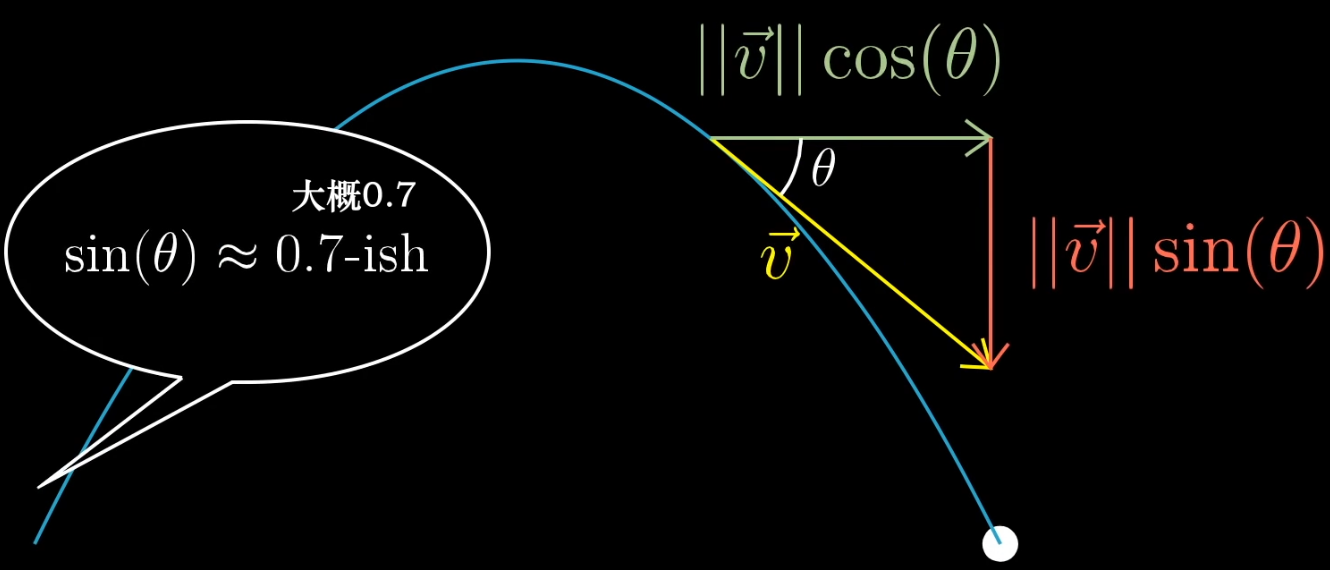
其实,你需要只是一个几何直观的灌输而已,这也从侧面佐证了一个好的老师或教材(这里的好老师真的不是他本身的学术能力有多强,而在于他擅不擅长站在学习者的角度不断的修正教学方法)是有多么重要。
教学不同层次的人:初学、入门、掌握、理解,解释的角度,方式都完全不同。更加不幸的是,为了能更加通用的用理论来描述现实生活中的规律,人类已经做了很多工作,我们常说:越通用,越抽象,这对于初学者来说堪称一段噩梦。
上述例子可能比较极端,但只为强调一件事:直观理解很重要,或者说,学习方法很重要。好的学习方法即你如何直观的去理解(可能是几何的,或是现实中的具体例子)一个抽象的事物,并层次化的建立知识与知识间的联系,构建并健壮属于自己的知识图谱。个人观点是,这种学习方法是最高效的。它唯一的要求在于,需要一定的基础知识打底,一定的量变结合方法论(点拨或领悟)就是质变。
向量究竟是什么
The introduction of numbers as coordinates is an act of violence.
引入一些数作为坐标是一种鲁莽的行为。
不同视角下的向量
对于向量的这个概念,大家一定并不陌生,但是这次让我们从数学,物理,计算机三个角度来看待如何定义这个向量这个概念。
物理专业角度
- 向量是空间中的箭头
- 决定一个向量的是:它的长度和它所指的方向
计算机专业角度
- 向量是有序的数字列表
- 向量不过是“列表”一个花哨的说法
- 向量的维度等于“列表”的长度
数学专业角度
对数学来说,它的本质就是通用和抽象,所以,数学家希望概括这两种观点:
- 向量可以是任何东西,只需要保证:两个向量相加及数字与向量相乘有意义
这里需要澄清一个重要的概念:数乘(也称为标量乘法)指的是用一个标量(即普通的数字,没有方向)去乘以一个向量(有大小和方向)。例如,数字3乘以向量\(\vec{v}\),结果是将向量\(\vec{v}\)的长度放大3倍,但方向保持不变。如果乘以负数,比如-2,那么向量长度放大2倍的同时,方向会完全相反。
- 向量加法和数乘贯穿线性代数始终,十分重要
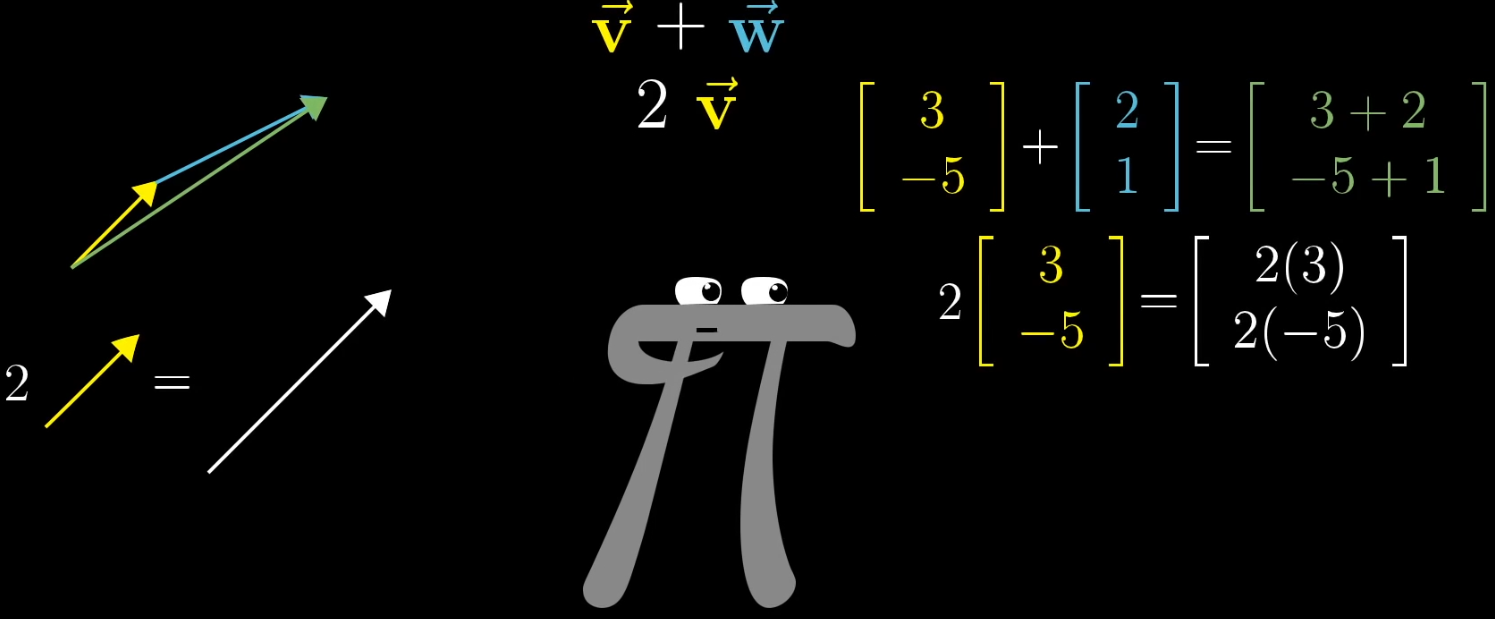
可以通过上图直观的感受到数学家在想什么。左边是物理角度,右边是计算机角度,但是很抱歉,我能用一些抽象的定义和约束让你们变成一个东西。
坐标系
把向量置于坐标系中,以原点为起点,坐标正负表示方向,可完美把两个不同的角度融合。
- 向量加法
- 物理:首尾相连 (Motion)
- 计算机:坐标相加
- 数乘
- 物理:缩放 (Scaling)
- 计算机:坐标和比例相乘
实际上无论你怎么看待向量都无所谓,或把向量看作空间中的箭头,或把向量看作数字列表,线性代数的效用很少体现在这些观点中的其中一个上,而是更多的体现在它能够在这些观点中互相转化。线性代数为数据分析提供了一条将大量数据列表概念化、可视化的渠道,它能让数据样式变得非常明晰,并让你大致了解其特定运算的意义。同时,线性代数给物理学家和计算机图形程序员提供了一种方法去通过计算机能处理的数字来描述并操纵空间(例如Mathematical Animation Engine)。
线性组合、基与其张成的空间
Mathematics requires a small dose, not of genius, but of an imaginative freedom which, in a larger dose, would be insanity. 数学需要的不是天赋,而是少量的自由想象,但想象太过自由又会陷入疯狂。
本部分继续加深一个概念,为何向量加法与数乘是那么重要,并从始至终贯穿整个线性代数(关于后面的直观解释部分,强烈建议去原视频观看动画演示)。
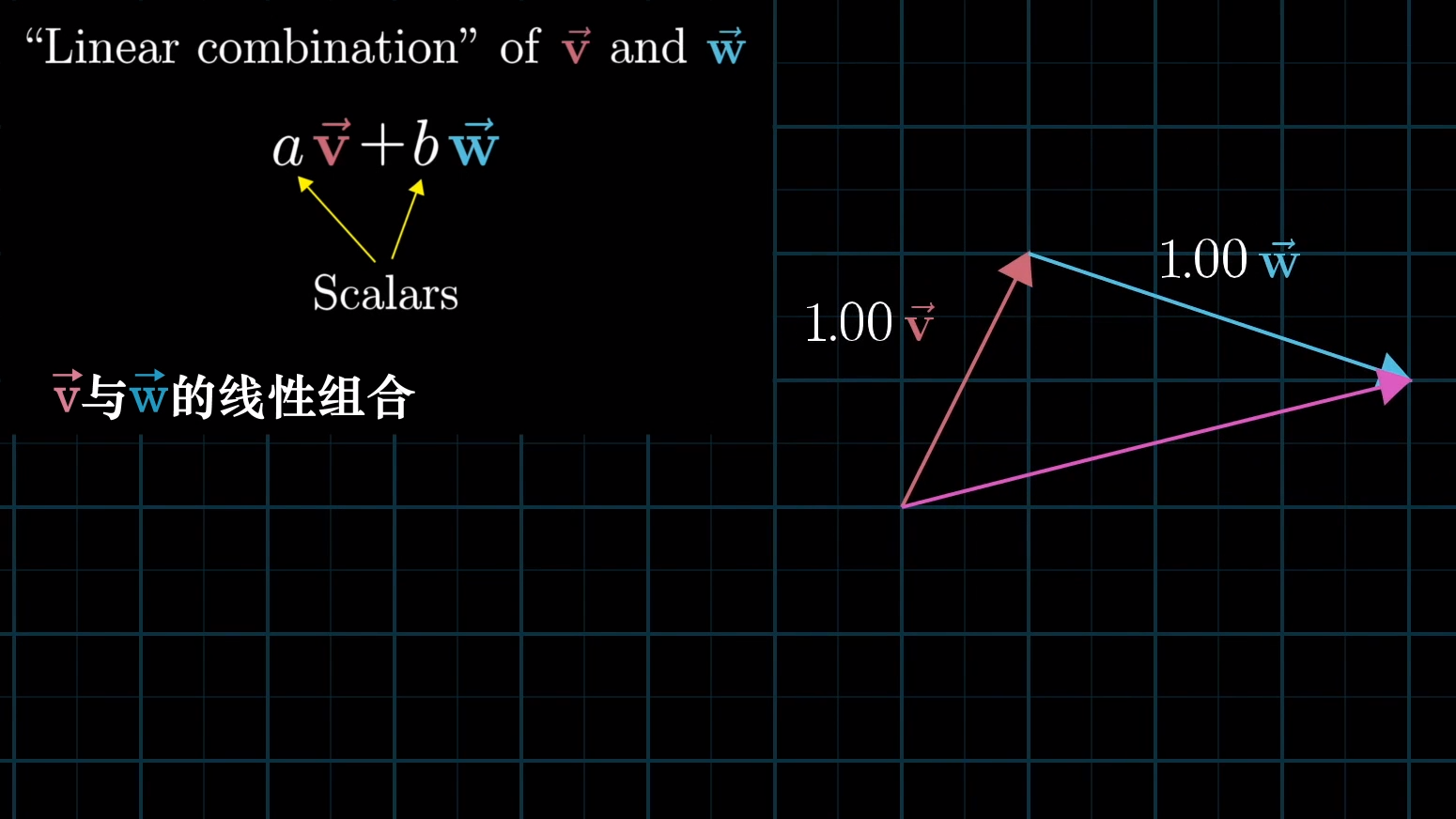
线性组合
二维空间中任意两个不共线的非零向量都可以表示该空间中的任意一个向量,写成符号语言就是:\(a \mathbf{\vec v} + b \mathbf{\vec w}\) 。
至于为什么被称为“线性”,有一种几何直观:如果你固定其中一个标量,让另一个标量自由变化,所产生的向量终点会描出一条直线。(这里其实很不严谨,具体定义请参阅课本。)
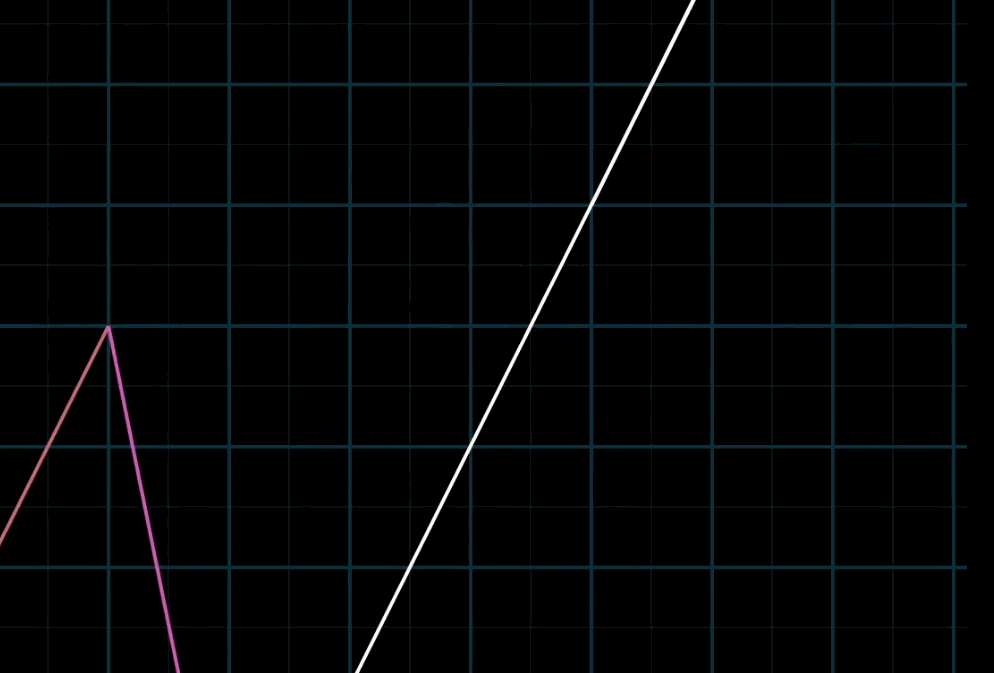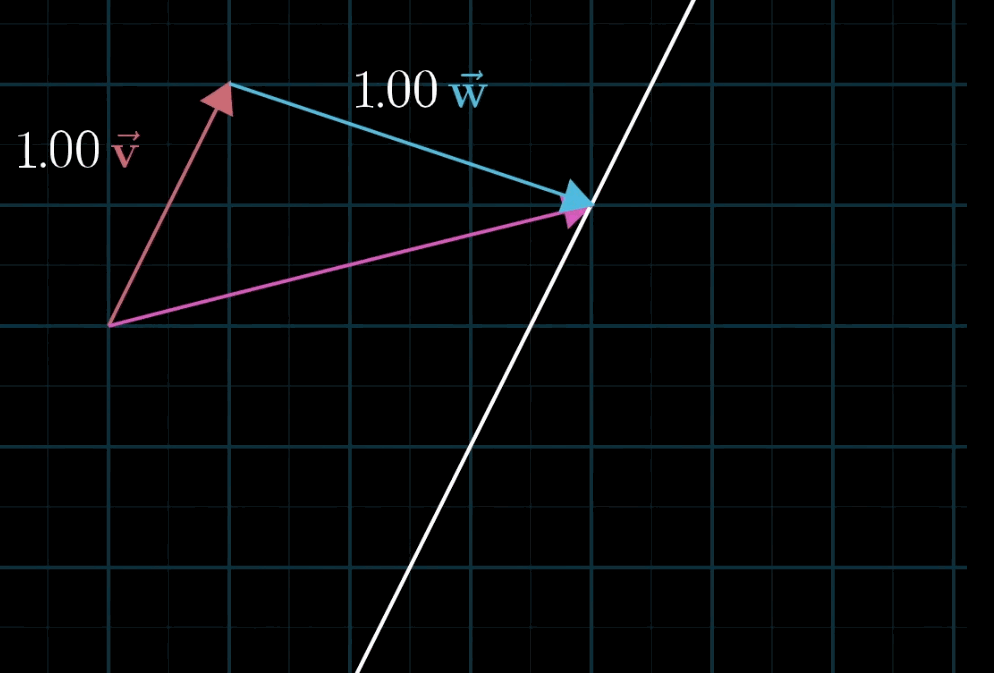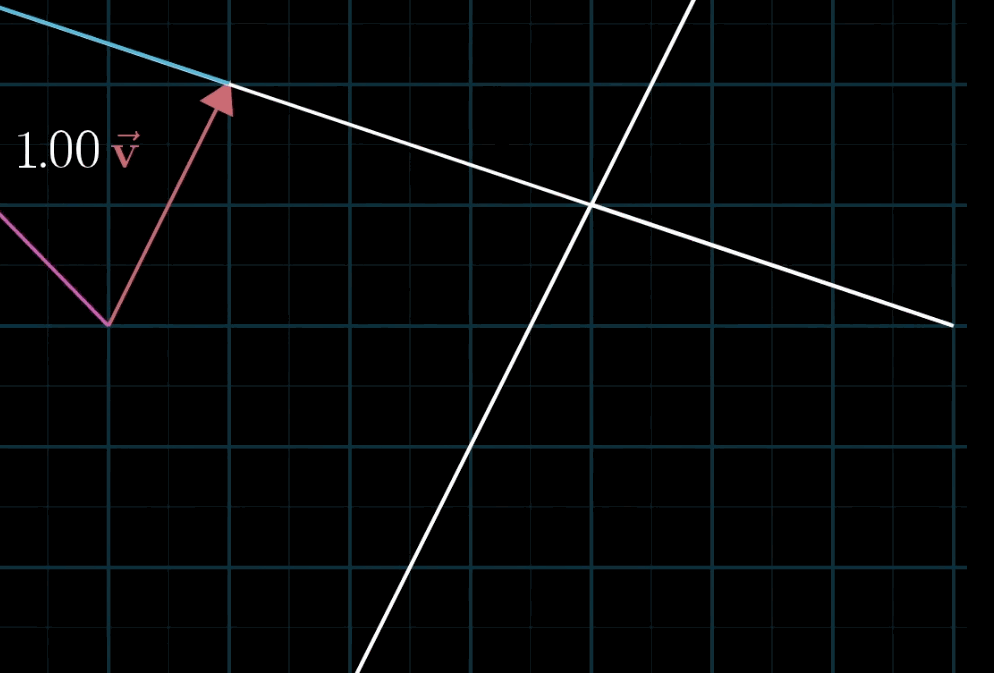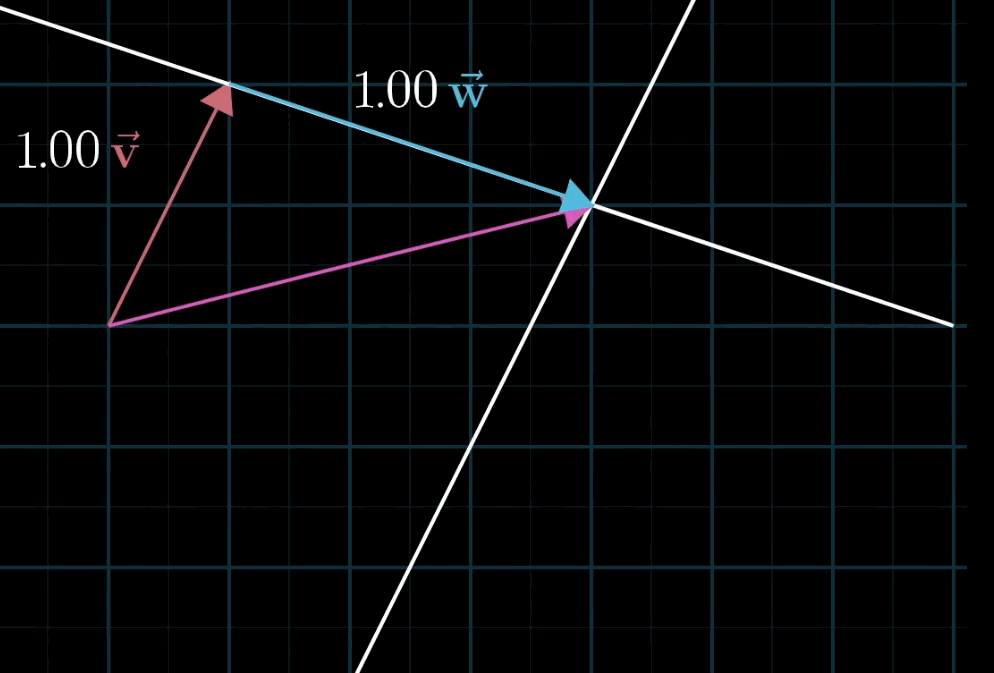
空间的基 (Basis)
对于我们常见的笛卡尔坐标系,有一组最直观的基:\(\{\hat{\imath}, \hat{\jmath}\}\),即单位向量 \(\hat{\imath}=(1,0)\) 和 \(\hat{\jmath}=(0,1)\) ,通过 \(\hat{\imath}\) 和 \(\hat{\jmath}\) 的拉伸与相加可以组成笛卡尔坐标系中的任意一个向量。(上述的任意两个不共线的非零向量也可以作为二维空间的一组基。)
张成的空间 (Span)
同理,我们可以选择不同的基向量,而这些基向量构成的空间就称为其张成的空间。张成二字比较拗口,可以类比为延伸或扩展。直观来看,就是本文所有图中的网格。笛卡尔坐标系就是一个由单位坐标 \(\{ \hat{\imath},{\hat{\jmath}} \}\) 张成的空间(同时也是上述任意两个不共线的非零向量所张成的空间)。所有可以表示为给定向量(基)线性组合(刚刚讲了这个概念)的向量的集合,被称为给定向量(基)张成的空间。
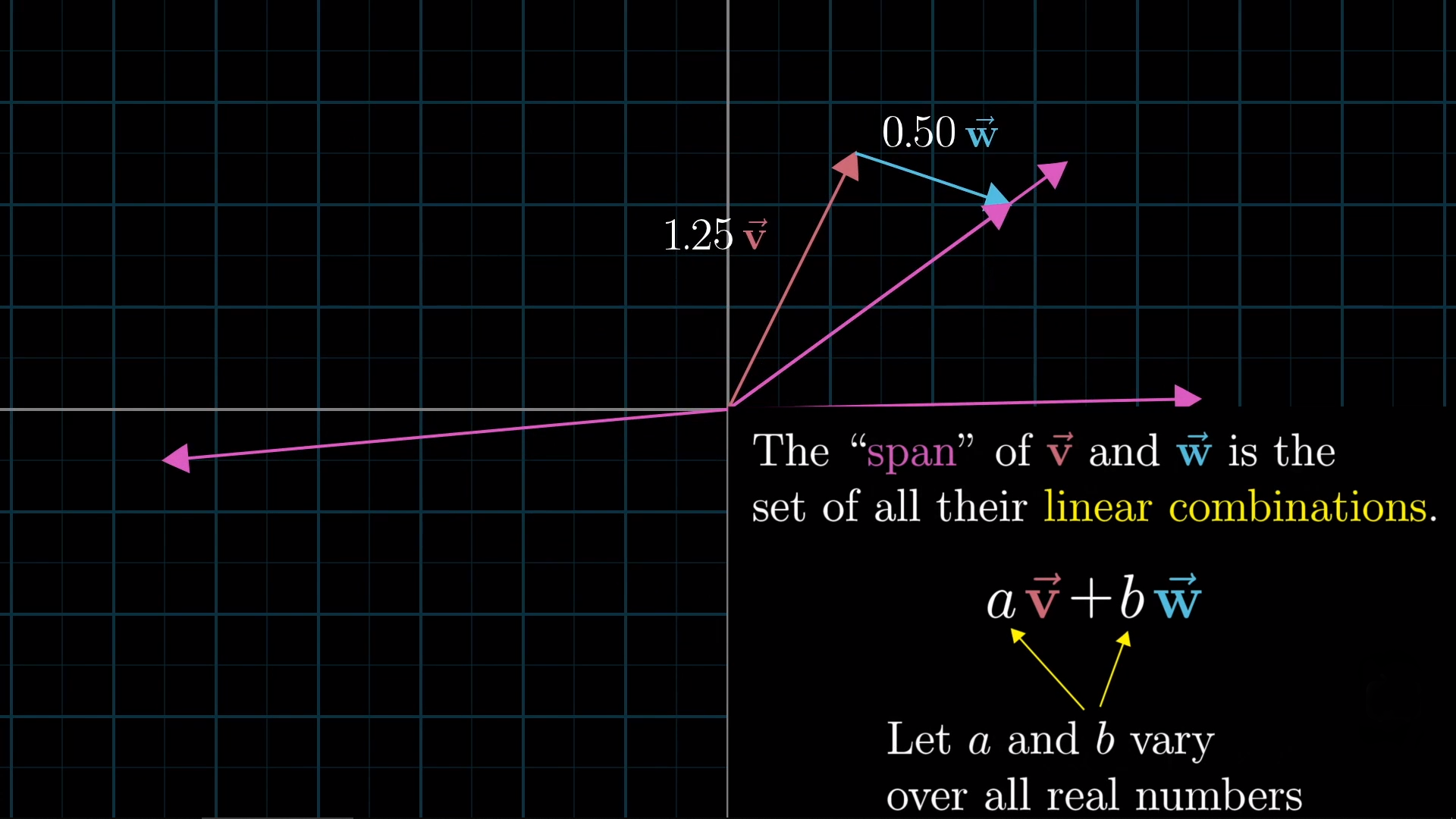
如果你继续思考一下,会发现一个特点:并不是每一组给定向量都可以张成一个空间,若这两个向量共线(2D),共面(3D),它们就只能被限制在一个直线或面中,类似于“降维打击”(这也是我强调不共线且向量非零的原因)。通过这个直观的思考可以引出以下概念:
线性相关
关于什么是线性相关,有两种等价的表达:
- 你有多个向量,并且可以移除其中一个而不减小张成的空间(即2D中共线或3D中共面),我们称它们(这些向量)线性相关。
- 其中一个向量,可以表示为其他向量的线性组合,因为这个向量已经落在其他向量张成的空间之中。
从统计学角度来说,就是指这些向量之中有冗余。即在这一堆向量中,我们只需要其中几个(取决于维度)就可以表示所有其他的向量。
由此,我们可以得出以下部分:
向量空间中一组基的严格定义
向量空间的一组基是张成该空间的一个线性无关向量集。
在线性代数中,基(basis)(也称为基底)是描述、刻画向量空间的基本工具。向量空间的基是它的一个特殊的子集,基的元素称为基向量。向量空间中任意一个元素,都可以唯一地表示成基向量的线性组合。如果基中元素个数有限,就称向量空间为有限维向量空间,将元素的个数称作向量空间的维数。 使用基底可以便利地描述向量空间。
用这样的步骤来慢慢导出这个定义,个人感觉,远比在课堂的第一分钟就将这句让你迷惑的话丢给你好的多,抽象的东西只有在慢慢推倒中你才能发现它的精巧之处,非常优雅且迷人。
矩阵与线性变换
Unfortunately, no one can be told what the Matrix is. You have to see it for yourself.
很遗憾,矩阵是什么是说不清的。你必须得自己亲眼看看。
矩阵,最直观的理解当然是一个写成方阵的数字 \(\begin{pmatrix}1&0 \\\ 0&1 \end{pmatrix}\) ,这几节的核心是为了说明:矩阵其实就是一种向量变换(至于什么是变换下面会讲),并附带一种不用死记硬背的考虑矩阵向量乘法的方法。
变换
变换本质上是函数(下左图)的一种花哨的说法,它接受输入内容,并输出对应结果,特别的,在矩阵变换(下右图)中,我们接受一个向量并且输出另一个向量。

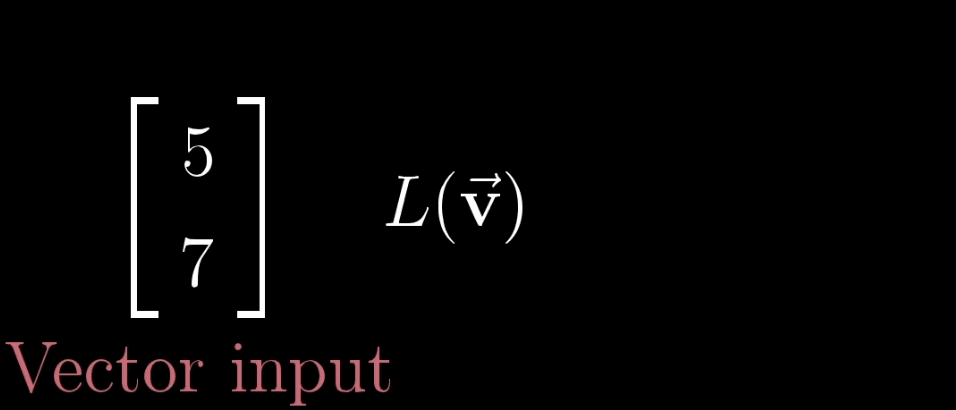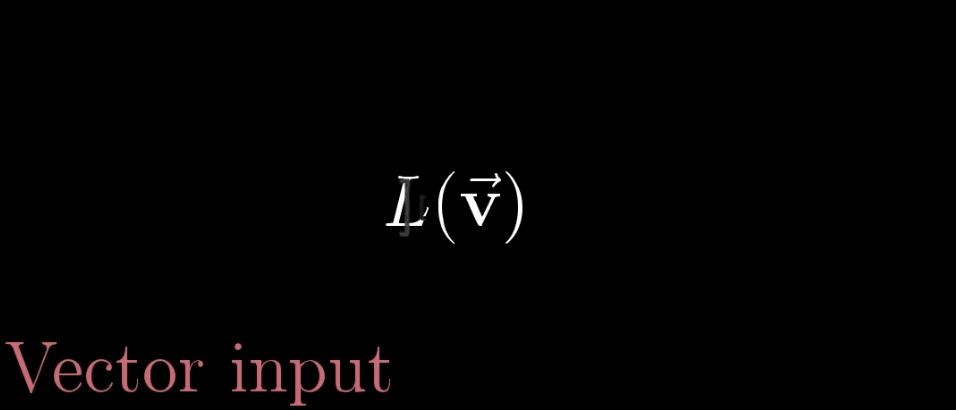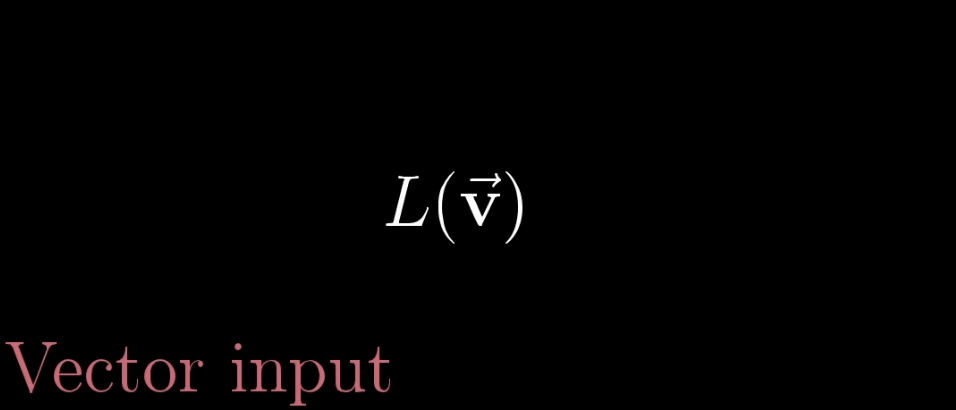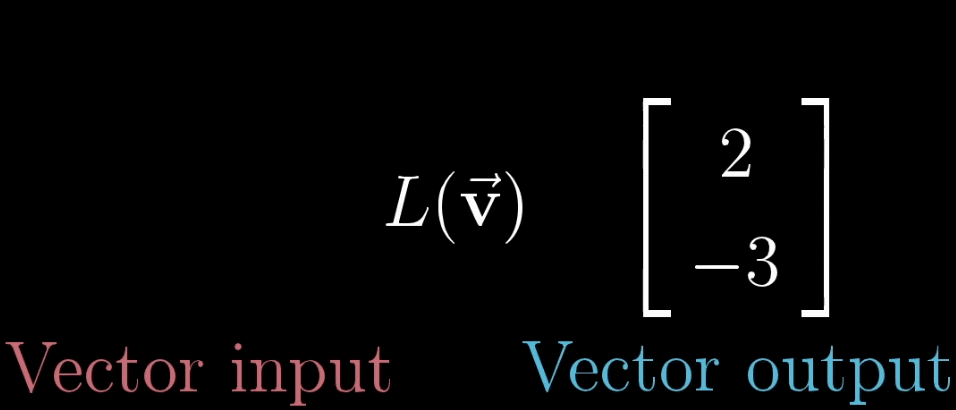
那既然变换和函数意义相同,为什么要用多余的术语困惑我们呢?因为使用变换是在暗示以特定方式来可视化这一输入\(\to\)输出关系。一种理解“向量的函数”的方法就是就是使用运动。
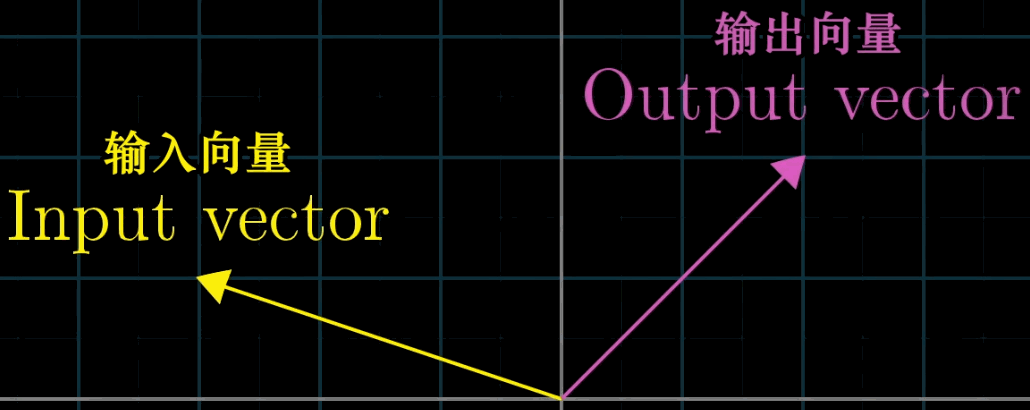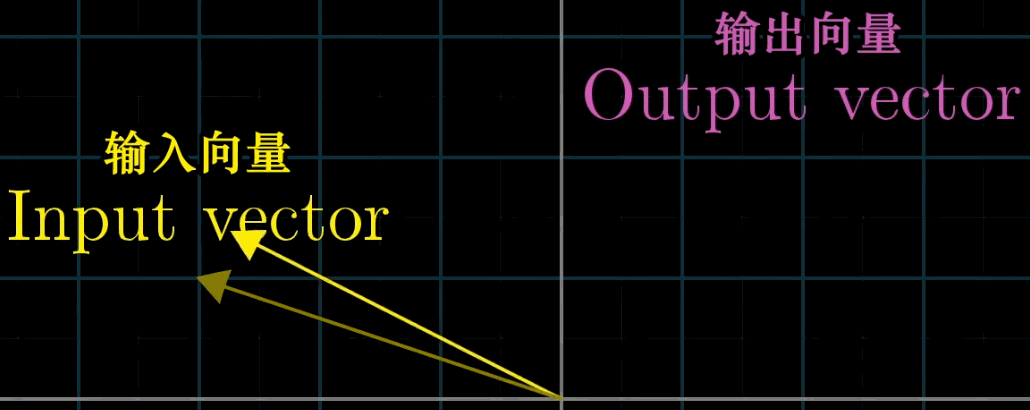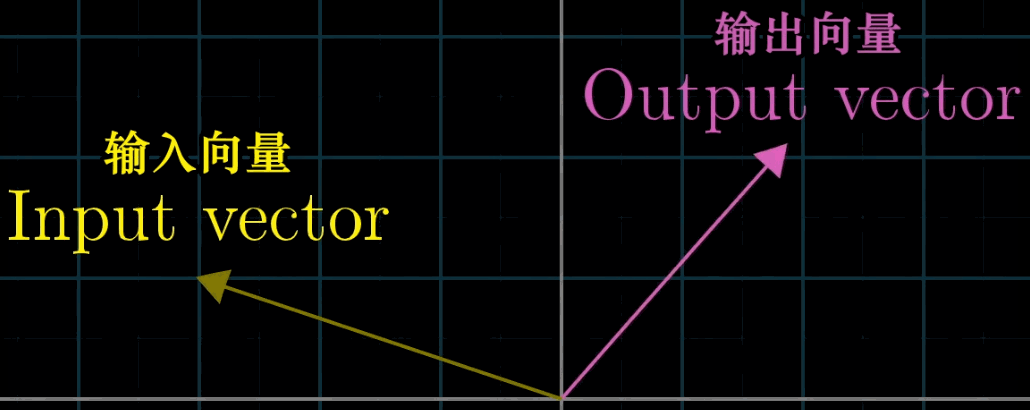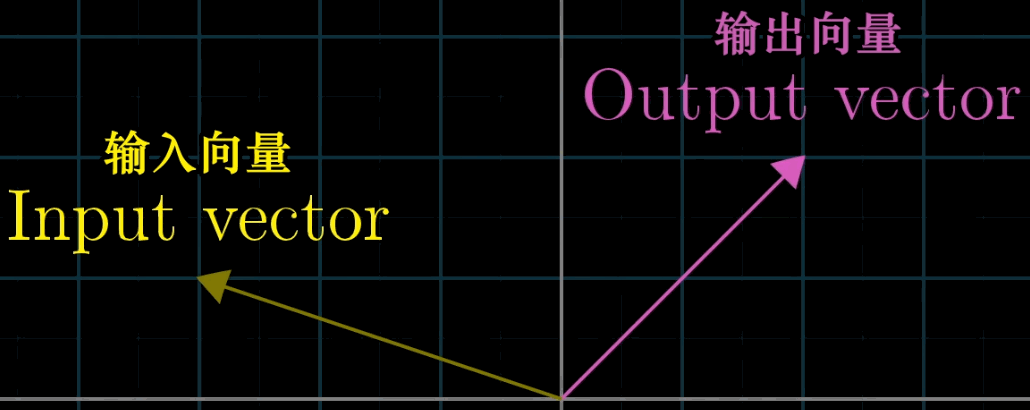
这世界上有非常多优美的变换,如果你将他们可视化,就能得到下图:

线性变换
我们说具有以下两个性质的就是线性变换(直观可视化如下图):
- 直线在变换后仍然保持为直线,不能有所弯曲。
- 原点必须保持固定

用一句话总结就是:线性变换是保持网格线平行且等距分布的变换(如果变换后保持直线不变但原点改变则为仿射变换,即线性变换+平移)。
如何用数值描述线性变换
这里需要使用上一节提到的工具,空间的基,也就是单位向量(基向量):\(\hat{\imath}=(1,0)\) 和 \(\hat{\jmath}=(0,1)\)
对线性变换,我们只需要关注两个基向量 \(\hat{\imath}\) 和 \(\hat{\jmath}\) 变换后的位置即可。例如,\(\hat{\imath}\) 变换到 \((3,1)\) 的位置,\(\hat{\jmath}\) 变换到 \((1,2)\) 的位置,将 \(\hat{\imath}\) 变换后的坐标竖起来作为方阵的第一列(绿色表示), \(\hat{\jmath}\) 变换后的坐标竖起来作为方阵的第二列(红色表示),得到矩阵 \(\begin{pmatrix}\color{green}3&\color{red}1 \\\ \color{green}1&\color{red}2 \end{pmatrix}\) 。假设我们想要知道目标向量 \((-1,2)\) 进行变换后的位置,那么这个矩阵就是对变换过程最好的描述。
- Step1: 绿色 \(\hat{\imath}\)(x轴)进行移动(变换)
- Step2: 红色 \(\hat{\jmath}\)(y轴)进行移动(变换)
- Step3: 目标向量x轴坐标值与 \(\hat{\imath}\) 变换后向量进行数乘
- Step4: 目标向量y轴坐标值与 \(\hat{\jmath}\) 变换后向量进行数乘
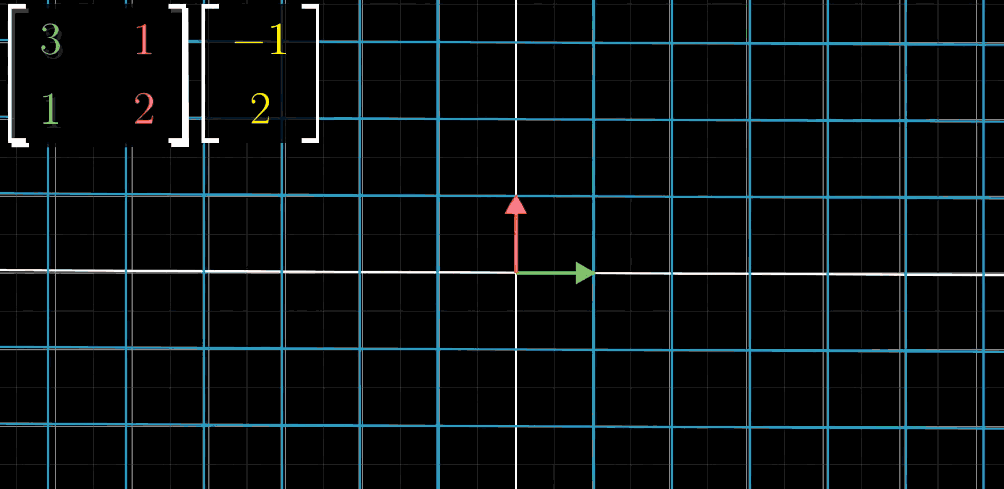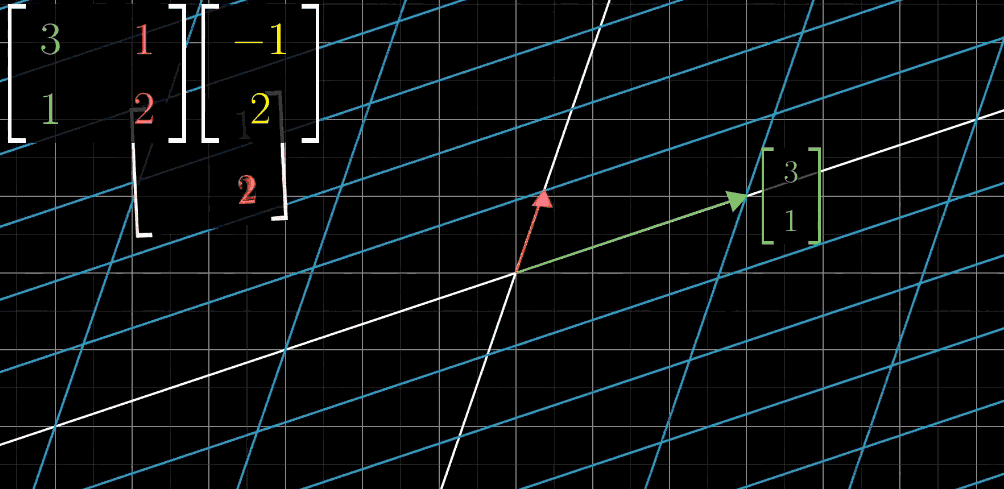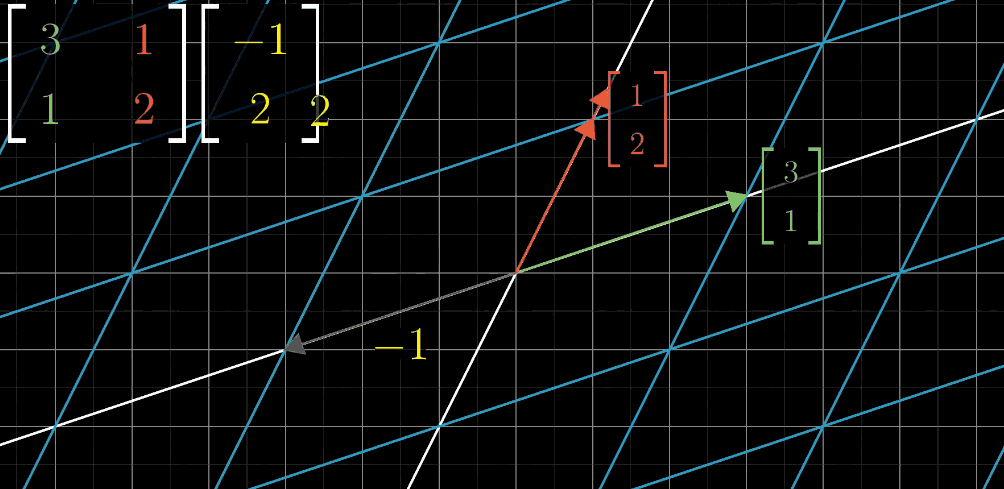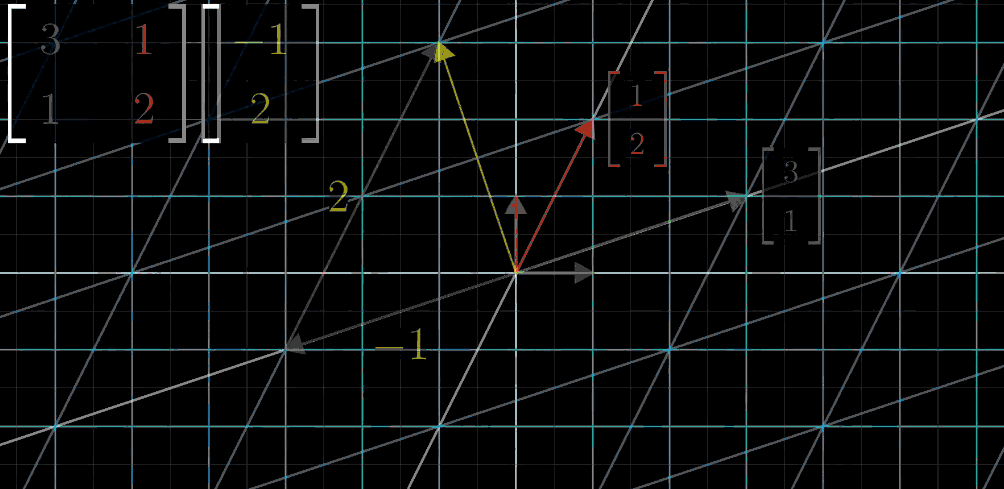
- Step5: 两者进行向量加法,得到线性变换结果
更加一般的情况,我们用变量来代替其中的具体值,其中绿色代表\(\hat{\imath}\)变换后的向量,红色代表\(\hat{\jmath}\)变换后的向量:
\[ \begin{pmatrix}\color{green}a&\color{red}b \\\ \color{green}c&\color{red}d \end{pmatrix}\begin{pmatrix} x \\\ y\end{pmatrix} = \underbrace{x \begin{pmatrix}\color{green}a \\\ \color{green}c \end{pmatrix} + y \begin{pmatrix} \color{red}b \\\ \color{red}d \end{pmatrix}}_{\text{直观的部分这里}} = \begin{pmatrix}\color{green}{a}\color{black}{x}+\color{red}{b}\color{black}{y} \\\ \color{green}{c}\color{black}{x}+\color{red}{d}\color{black}{y}\end{pmatrix} \]
上面的公式就是我们常说的矩阵乘法公式,现在,不要强行背诵,结合可视化的直观动图,你一辈子都不会忘记的。
线性的严格定义
在给出一个数学化抽象的解释前,先做一下总结:
- 线性变换是操纵空间的一种手段,它保持网格线平行且等距分布,并保持原点不动
- 矩阵是描述这种变换的一组数字,或者说一种描述线性变换的语言
在数学上,线性的严格定义如下述公式,这些性质,会在之后进行讨论,也可以在这里就进行一些思考,为什么说向量加法和数乘贯穿线性代数始终?
\[ \begin{align*} L(\mathbf{\vec v} + \mathbf{\vec w}) &= L(\mathbf{\vec v}) + L(\mathbf{\vec w}) \qquad \text{可加性(对加法封闭)} \\ L(c\mathbf{\vec v}) &= cL(\mathbf{\vec v}) \qquad \text{齐次性(对标量乘法封闭)} \end{align*} \]
矩阵乘法与线性变换复合
It is my experience that proofs involving matrices can be shortened by 50% if one throws the matrices out.
据我的经验,如果丢掉矩阵的话,那些涉及矩阵的证明可以缩短一半。
复合变换
如果对一个向量先进行一次旋转变换,再进行一次剪切变换(\(\hat{\imath}\) 保持 \((1,0)\) 不变,\(\hat{\jmath}\) 移动到坐标 \((1,1)\)),如下图所示:

那么如果通过旋转矩阵和剪切矩阵来求得这个符合矩阵呢?为了解决这个问题,我们定义这个过程叫做矩阵的乘法。
矩阵乘法的计算
在这里我们发现,矩阵乘法的变换顺序是从右往左读的(这一个常识很重要,你得明白这一点,有基本概念),也和我们熟知的复合函数形式 \(f(g(x))\) 是一致的。
那么如何求解矩阵乘法呢?对线性代数有印象的同学现在能马上记起来那个稍显复杂的公式吗?如果有些忘记了,那么,现在,就有一个一辈子也忘不了的直观解释方法:
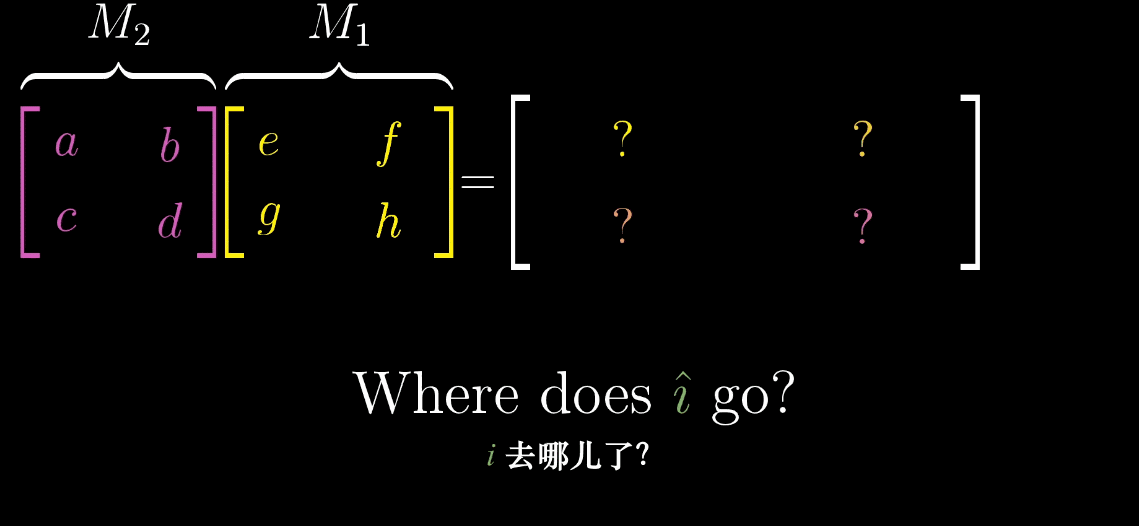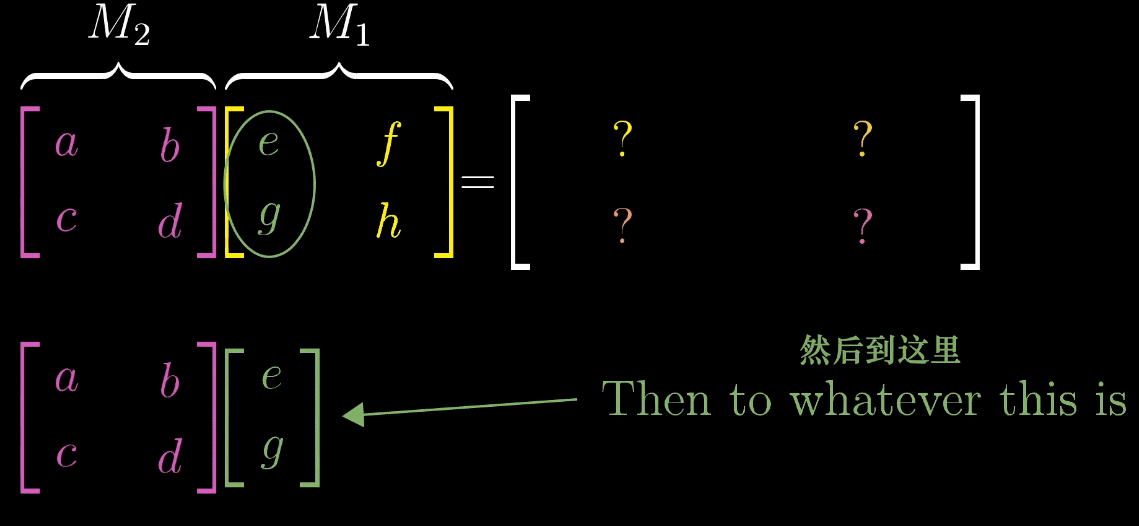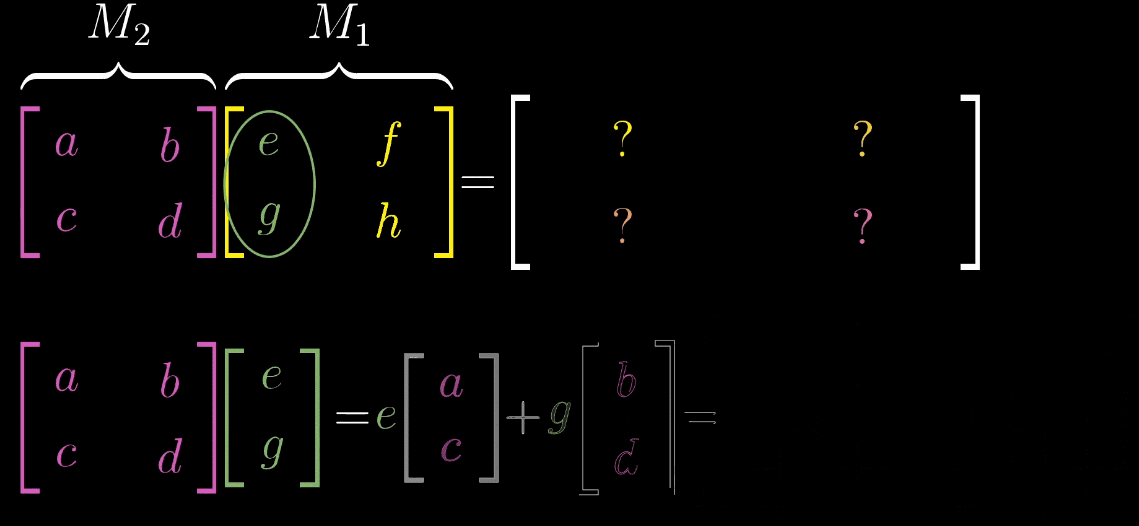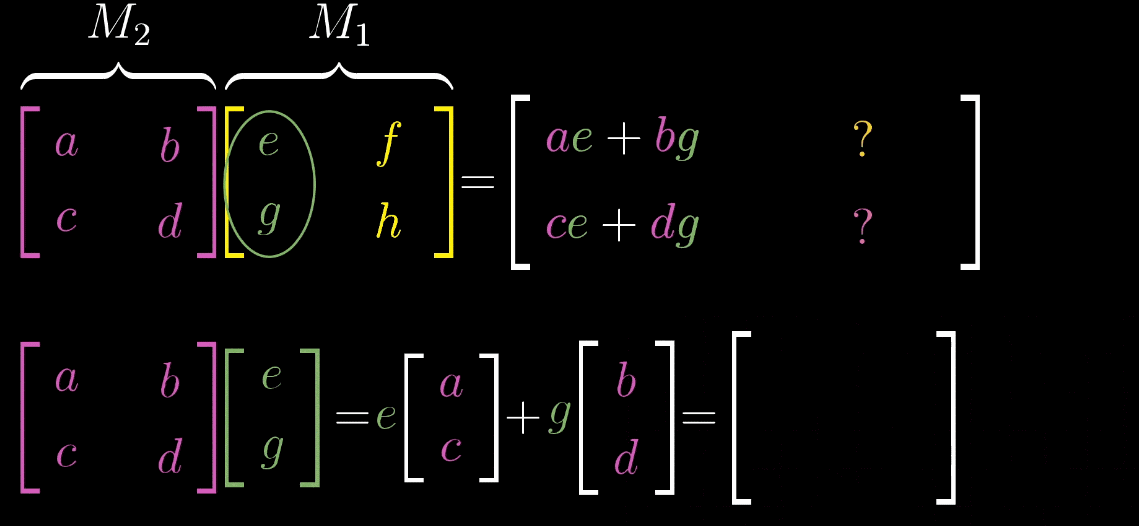
如图,\(M_1\) 矩阵的第一列表示的是 \(\hat{\imath}\) 变换的位置,先把它拿出来,\(M_2\) 矩阵看成对这个变换过的 \(\hat{\imath}\) 进行一次变换(按照前文的规则)。同理,针对 \(\hat{\jmath}\) 做一样的操作,就可以得出这个表达式。
矩阵乘法的运算规律
通常学生在学习矩阵乘法时都会记住上述公式并通过一些特定的运算加强记忆(包括我),但是在记忆这个过程前,我希望你能养成思考矩阵乘法意义的习惯,也就是两个变换相继作用。这能形成一个更好的概念性框架,并让你更容易理解矩阵乘积的性质。
举个栗子,矩阵相乘时,它们的先后顺序影响结果吗?有了上面的想法,可以自己试着在不进行计算的条件下思考一下,然后再尝试证明结合律与分配律是否成立。你会发现,原来线性代数是这么的直观,完全不需要计算。而三维空间内扩展的话,你会发现,显示生活中的每一种形态改变都能用一个3×3的矩阵来表示这个变换,这在机器人或自动化操作领域是非常重要的,因为你可以把现实生活很难描述的动作通过一个矩阵来表示,是一个连接数字和现实的重要桥梁和工具。
行列式
The purpose of computation is insight, not numbers.
计算的目的不在于数字本身,而在于洞察其背后的意义。
行列式是线性代数中一个非常重要的概念,它不仅在数学理论中扮演着关键角色,而且在实际应用中也有着广泛的用途。在深入学习行列式之前,让我们先从几何直观的角度来理解它。
行列式的几何意义
在线性变换中,我们经常需要度量变换对空间的“拉伸”或“压缩”程度。考虑二维空间中的单位正方形,它由基向量 \(\hat{\imath}=(1,0)\) 和 \(\hat{\jmath}=(0,1)\) 张成,面积为1。当应用一个线性变换时,这个单位正方形会被变换为一个平行四边形。
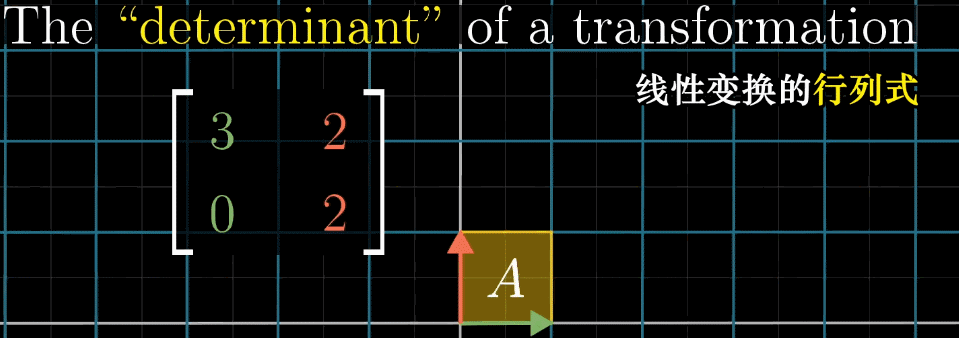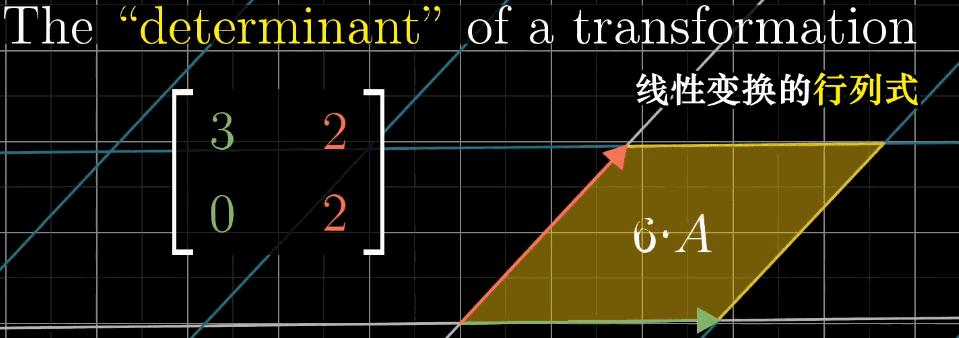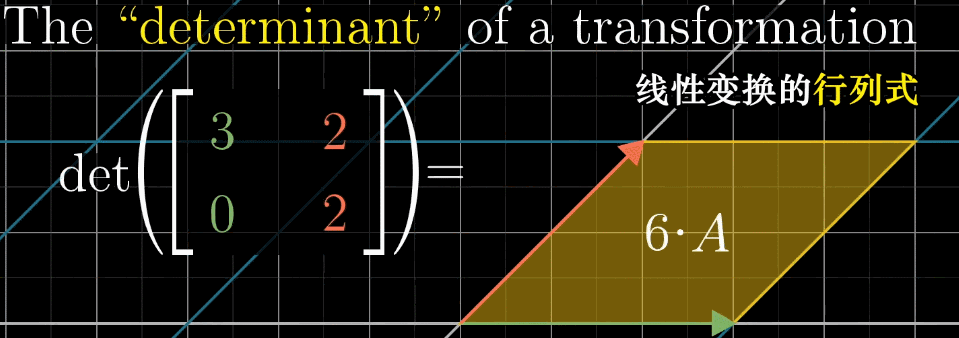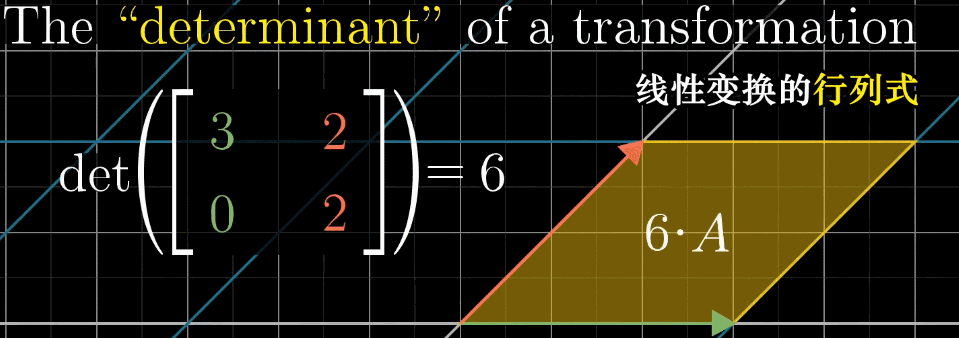
这个平行四边形的面积与原正方形面积的比值,就是这个线性变换的行列式的绝对值。换句话说,行列式度量了线性变换对面积的缩放比例。
需要注意的是,行列式不仅有大小,还有符号。行列式的正负表示变换是否改变了空间的定向:
- 当行列式为正时,空间的定向保持不变
- 当行列式为负时,空间被“翻转”了,定向发生了改变
在三维空间中,行列式表示线性变换对体积的缩放比例。
行列式的特殊情况
当行列式为0时,这意味着线性变换将空间压缩到了更低的维度上。例如,在二维情况下,变换将整个平面压缩到一条直线上,甚至是一个点上。这种情况对应于矩阵的列向量线性相关。
从几何角度理解,当行列式为0时,说明变换后的基向量共线(二维情况)或共面(三维情况),因此它们无法张成完整的空间维度。
二维行列式的计算
对于一个 \(2 \times 2\) 的矩阵 \(\begin{pmatrix} a & b \\ c & d \end{pmatrix}\),其行列式的计算公式为:
\[ \det \begin{pmatrix} a & b \\ c & d \end{pmatrix} = ad - bc \]
这个公式可以通过几何直观来理解。考虑基向量 \(\hat{\imath}\) 和 \(\hat{\jmath}\) 变换后的位置 \((a,c)\) 和 \((b,d)\),它们张成的平行四边形面积就是 \(|ad - bc|\)。
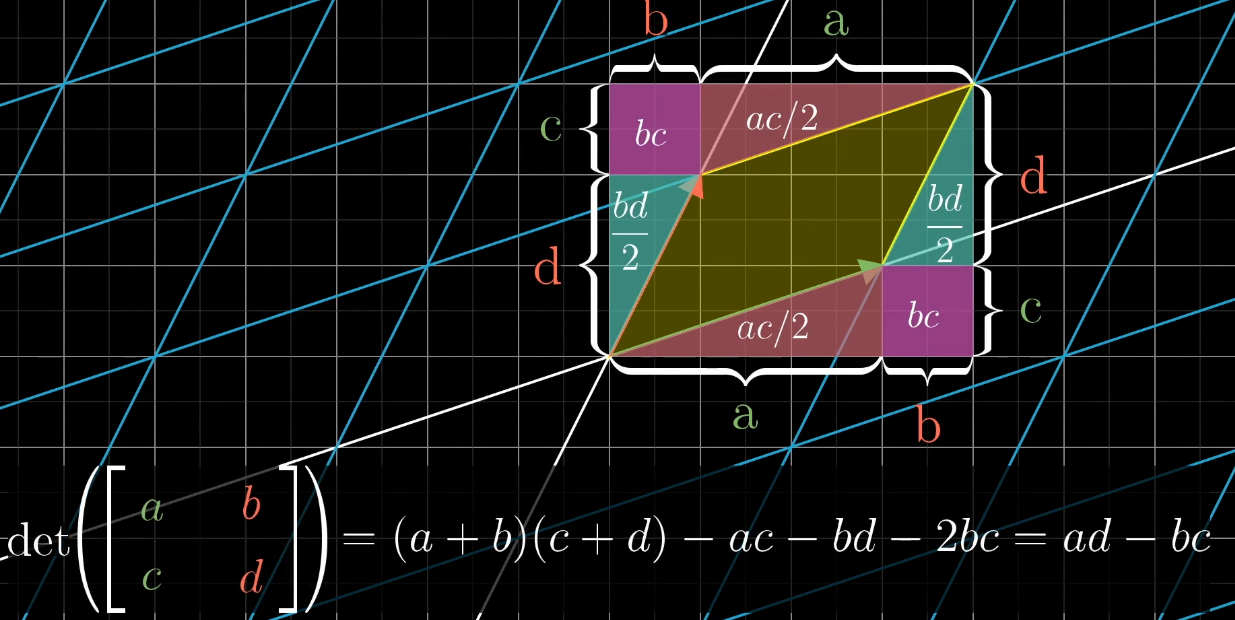
记忆这个公式的一个小技巧:沿着主对角线(从左上到右下)的元素相乘后相加,减去副对角线(从右上到左下)的元素相乘后的结果。
行列式的性质
行列式有许多重要性质,其中最值得注意的是:
\[ \det(M_1 M_2) = \det(M_1) \det(M_2) \]
这个性质的几何意义非常直观:对空间进行两次连续变换,总的缩放比例等于各次变换缩放比例的乘积。想象你先将一个橡皮泥拉伸2倍,然后再拉伸3倍,最终的效果就是拉伸6倍。
三维及高维行列式
在三维空间中,行列式表示由三个列向量张成的平行六面体的有向体积。对于 \(3 \times 3\) 矩阵,行列式的计算稍显复杂,但其几何意义保持一致:度量线性变换对体积的缩放比例。
对于更高维度,行列式继续推广这一概念,度量线性变换对高维体积的缩放比例。
行列式作为线性代数的核心概念之一,为我们提供了一个强有力的工具来理解线性变换的本质特性。在后续章节中,我们将看到行列式在求解线性方程组、计算逆矩阵等方面的重要应用。
逆矩阵、列空间与零空间
To ask the right question is harder than to answer it.
提出正确的问题比回答它更难。
在线性代数中,我们不仅要理解线性变换的本质,还要学会如何解决实际问题。逆矩阵、列空间和零空间是三个关键概念,它们在线性方程组的求解中发挥着重要作用。
线性方程组与逆矩阵
线性方程组是线性代数的核心应用之一。考虑一个简单的线性方程组:
\[ \begin{align*} ax + by &= e \\ cx + dy &= f \end{align*} \]
用矩阵形式可以表示为 \(A\mathbf{\vec{x}} = \mathbf{\vec{v}}\),其中 \(A = \begin{pmatrix} a & b \\ c & d \end{pmatrix}\),\(\mathbf{\vec{x}} = \begin{pmatrix} x \\ y \end{pmatrix}\),\(\mathbf{\vec{v}} = \begin{pmatrix} e \\ f \end{pmatrix}\)。
从几何角度理解,这个问题是在问:向量 \(\mathbf{\vec{x}}\) 经过矩阵 \(A\) 所表示的线性变换后,恰好落在向量 \(\mathbf{\vec{v}}\) 上的位置。要找到 \(\mathbf{\vec{x}}\),我们需要进行反向操作。

这个反向操作对应的变换就是矩阵 \(A\) 的逆矩阵,记作 \(A^{-1}\)。如果逆矩阵存在,则有:
\[ A^{-1}A\mathbf{\vec{x}} = A^{-1}\mathbf{\vec{v}} \implies \mathbf{\vec{x}} = A^{-1}\mathbf{\vec{v}} \]
换句话说,逆矩阵就是原变换的“撤销”操作,就像Ctrl+Z一样。
逆矩阵的几何意义
逆矩阵的几何意义非常直观:如果矩阵 \(A\) 将基向量 \(\hat{\imath}\) 和 \(\hat{\jmath}\) 变换到新的位置 \(\hat{\imath'}\) 和 \(\hat{\jmath'}\),那么逆矩阵 \(A^{-1}\) 的作用就是将 \(\hat{\imath'}\) 和 \(\hat{\jmath'}\) 变换回原来的位置 \(\hat{\imath}\) 和 \(\hat{\jmath}\)。
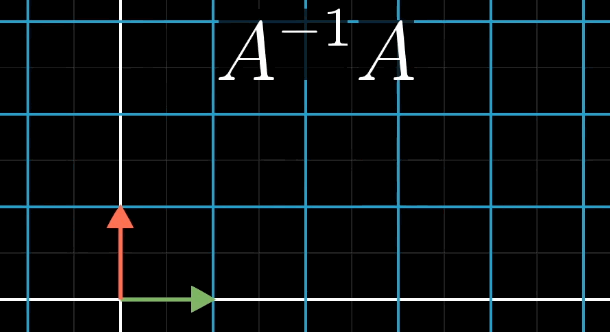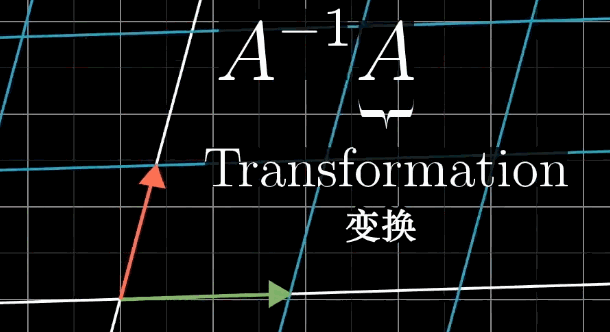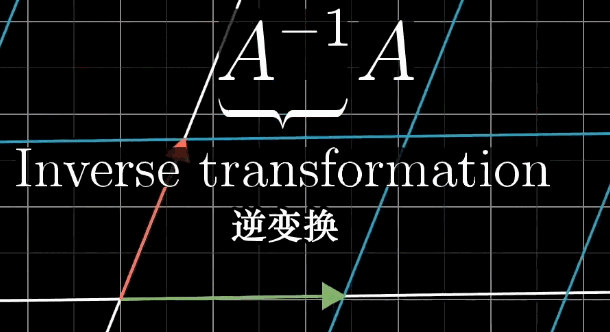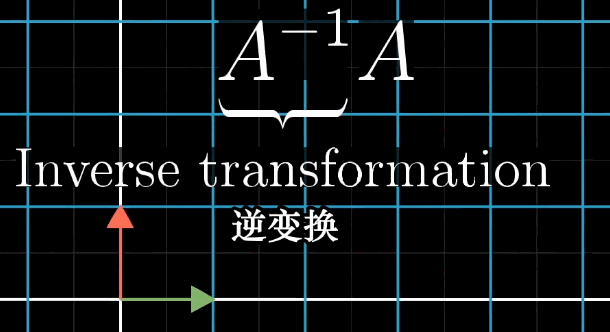
需要注意的是,逆矩阵存在的条件是 \(\det(A) \neq 0\)。当行列式为0时,线性变换将空间压缩到更低的维度上,这种压缩是不可逆的。这就像你把一张纸揉成一团,虽然你改变了它的形状,但你无法通过任何操作把它完全恢复成原来的样子。
列空间
矩阵的列空间(Column Space)是线性代数中另一个重要概念。对于矩阵 \(A\),其列空间是所有可能的输出向量 \(A\mathbf{\vec{v}}\) 构成的集合。
从几何角度来看,矩阵的列就是基向量变换后的位置。因此,列空间就是这些列向量所张成的空间。

列空间帮助我们理解线性方程组解的存在性:
- 当向量 \(\mathbf{\vec{v}}\) 在矩阵 \(A\) 的列空间中时,方程 \(A\mathbf{\vec{x}} = \mathbf{\vec{v}}\) 有解
- 当向量 \(\mathbf{\vec{v}}\) 不在矩阵 \(A\) 的列空间中时,方程无解
可以这样理解:列空间就是矩阵 \(A\) 能够“到达”的所有位置的集合。如果目标向量 \(\mathbf{\vec{v}}\) 在这个集合中,我们就能找到一个输入向量到达它;否则,无论怎么调整输入都无法到达目标位置。
秩
矩阵的秩(Rank)是衡量矩阵“信息量”的重要指标。从几何直观来看,矩阵的秩就是变换后空间的维度。
更精确地说,矩阵的秩等于其列空间的维度。例如:
- 满秩矩阵:秩等于矩阵的行数和列数中的较小值
- 降秩矩阵:秩小于矩阵的行数和列数中的较小值
零空间
零空间(Null Space)或核(Kernel)是另一个关键概念。它是指所有满足 \(A\mathbf{\vec{x}} = \mathbf{\vec{0}}\) 的向量 \(\mathbf{\vec{x}}\) 构成的集合,即变换后落在原点的向量集合。
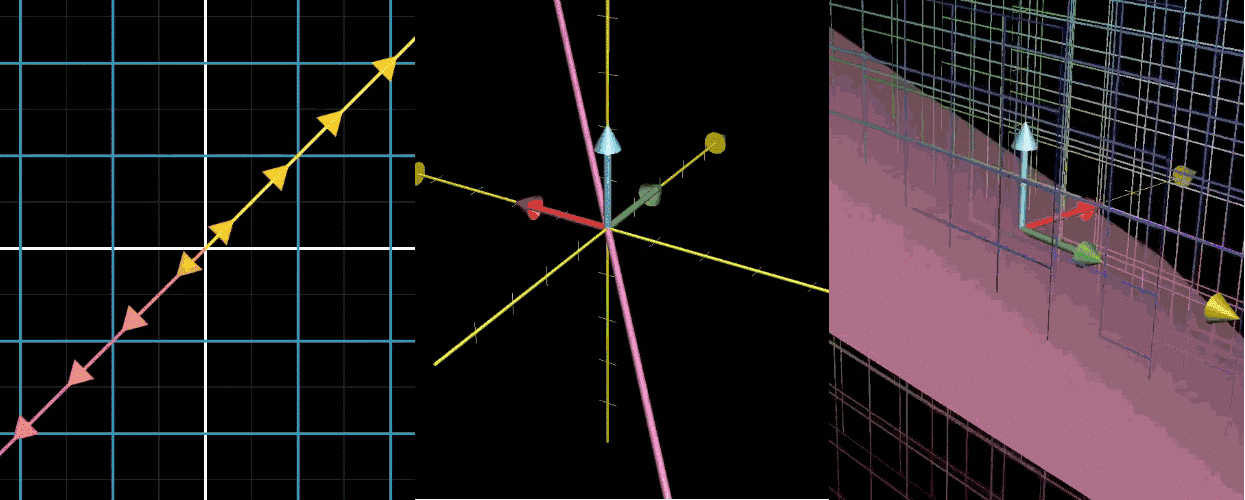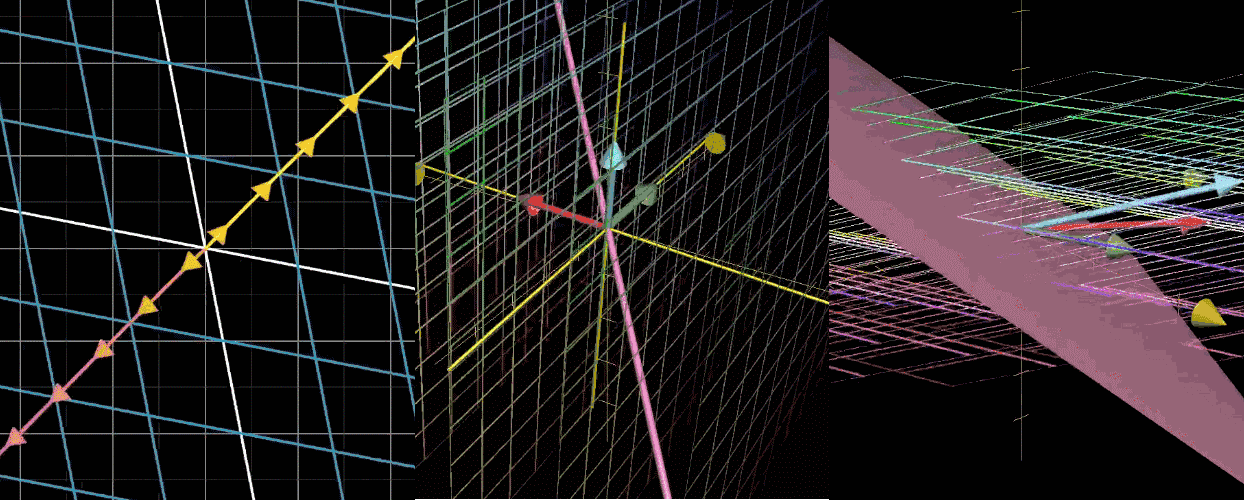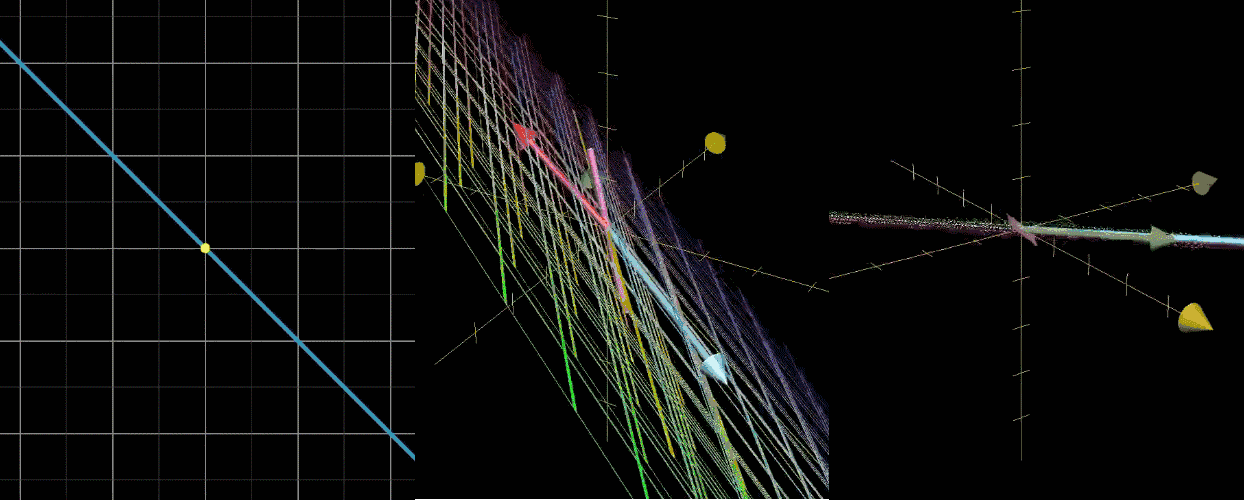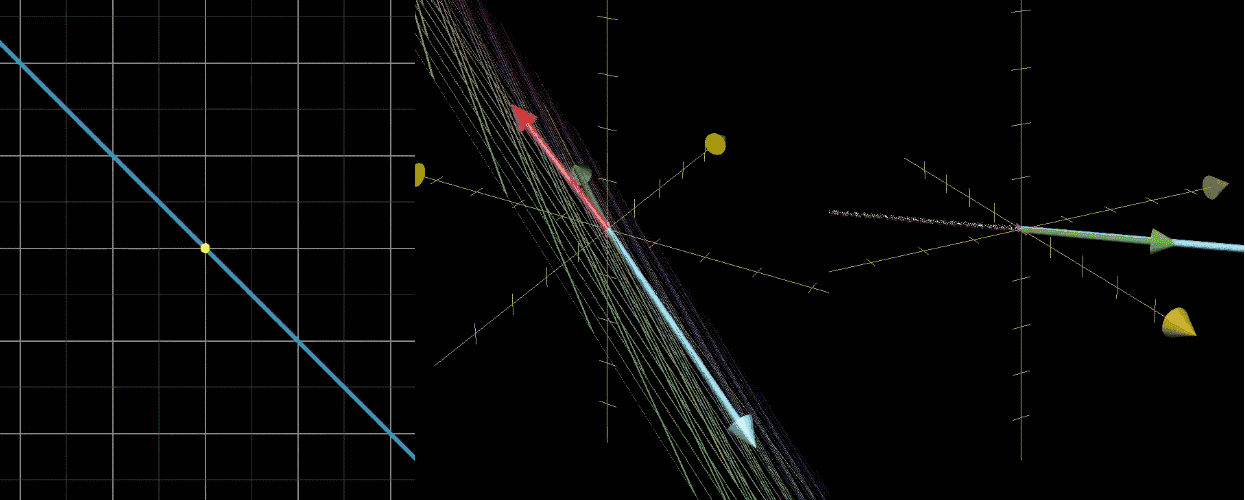
零空间的维度与矩阵的秩之间存在重要关系,这就是著名的秩-零化度定理: \[ \text{rank}(A) + \text{nullity}(A) = \text{列数} \]
直观理解:秩表示变换后保留了多少维度的信息,而零空间的维度表示有多少维度的信息在变换中“丢失”了(被压缩到原点)。
总结
逆矩阵、列空间和零空间这三个概念为我们提供了理解和解决线性方程组的完整框架:
- 逆矩阵帮助我们直接求解线性方程组
- 列空间告诉我们解的存在性
- 零空间描述了解的结构
这些概念不仅在理论研究中重要,在实际应用如机器学习、数据科学、工程计算等领域也有着广泛的应用。
通过几何直观理解这些概念,我们能够更深刻地把握线性代数的本质,而不仅仅停留在公式记忆层面。这种理解方式将帮助我们在面对复杂问题时找到更清晰的解决思路。
非方阵
在这个小测试里,我让你们求一个2×3矩阵的行列式。让我感到非常可笑的是,你们当中竟然有人尝试去做。
On this quiz, I asked you to find the determinant of a 2×3 matrix. Some of you, to my great amusement, actually tried to do this.
几何意义
首先从一个特例出发,考虑3×2(3行2列)矩阵的几何意义。从列空间我们得知,第一列表示的是 \(\hat{\imath}\) 变换后的位置(现在是一个有三个坐标的值,即三维),第二列同理是 \(\hat{\jmath}\)。总结来说,3×2矩阵的几何意义是将二维空间映射到三维空间上。
此时从特例到一般化推倒,我们可以得到一个结论:n*m 的几何意义是将m维空间(输入空间)映射到n维空间(输出空间)上。
注意这里的输入空间、输出空间的概念,阅读方向同样也是从右向左的(靠右的是输入,靠左的是输出)。
一个形象的比喻是:如果你有一个2D图像(比如一张照片),通过一个3×2矩阵变换,你就可以得到一个3D模型的投影。
非方阵乘法
如果你已经学过线性代数的大学课程,你可能有一些印象,并不是任意两个非方阵都可以进行矩阵乘法,必须满足一些条件。例如,在 \(M_1M_2\)(非方阵)计算中,假设 \(M_2\) 为2×3的矩阵,那么 \(M_1\) 的列必须等于 \(M_2\) 的行,否则这个乘法是没法计算的。
当我们有了变换的几何直观后,这个概念只要自己思考推导一次,也是一辈子都忘不了的。
直观解释是:矩阵的行是这个变换的输出空间维数,而列是变换的输入空间维数。矩阵乘法从右向左读,第一个变换 \(M_2\) 的输出向量的维度(\(M_2\) 的行)必须和第二个变换 \(M_1\) 的输入向量(\(M_1\) 的列)维度相等,才可以计算。也就是说,类似于插头和插座的关系,我只有三头插座,你来一个双头插头肯定没法用的。
这就像函数的复合一样,\(f(g(x))\)中,\(g(x)\)的输出必须与\(f\)的输入类型匹配。
非方阵行列式
这里有一个很好玩的概念,非方阵的行列式呢?都不是一个维度的变换,如同归零者和咱们谈判一样,你和我谈缩放比例?不存在的。
这是因为行列式的本质是度量变换对空间体积的缩放比例,而非方阵代表的是不同维度空间之间的变换,无法直接比较“体积”的变化。
点积与对偶性
卡尔文:你知道吗,我觉得数学不是一门科学,而是一种宗教。
霍布斯:一种宗教?
卡尔文:是啊。这些公式就像奇迹一般。你取出两个数,把它们相加时,它们神奇地成为了一个全新的数!没人能说清这到底是怎么发生的。你要么完全相信,要么完全不信。
什么是点积
对两个相同维数的向量,或是两个相同长度的数组。求它们的点积,就是将相应坐标配对,求出每一对坐标的乘积,然后将结果相加。
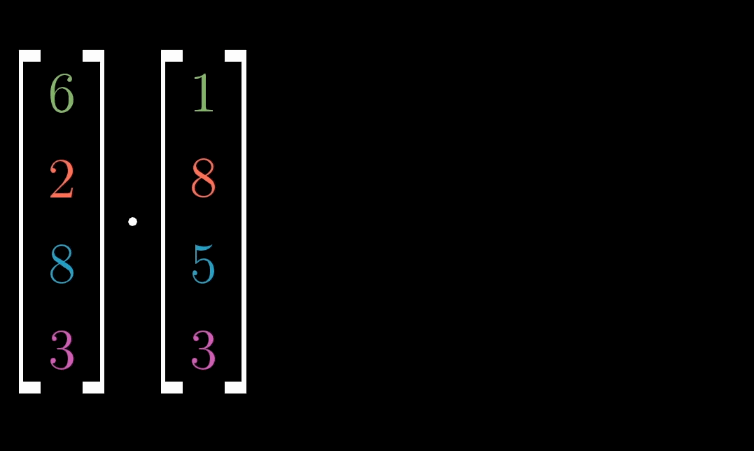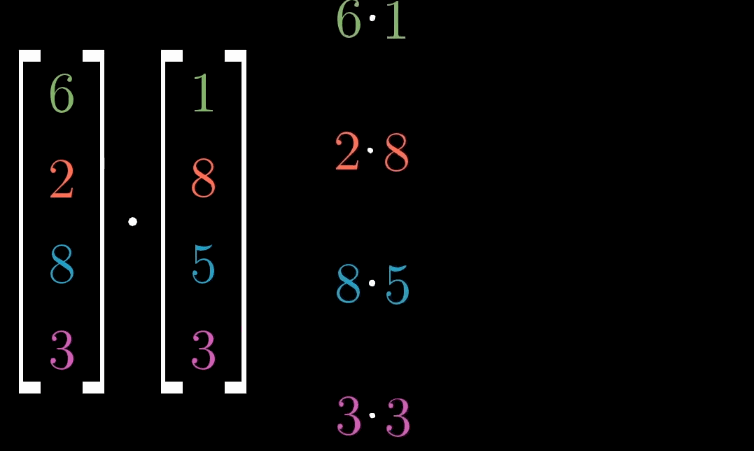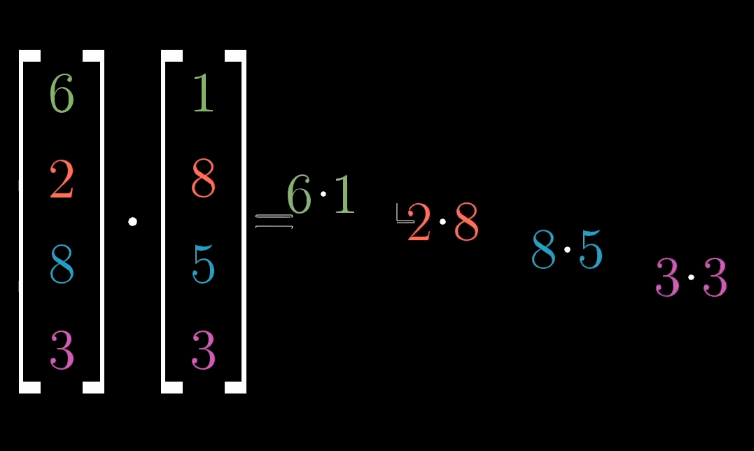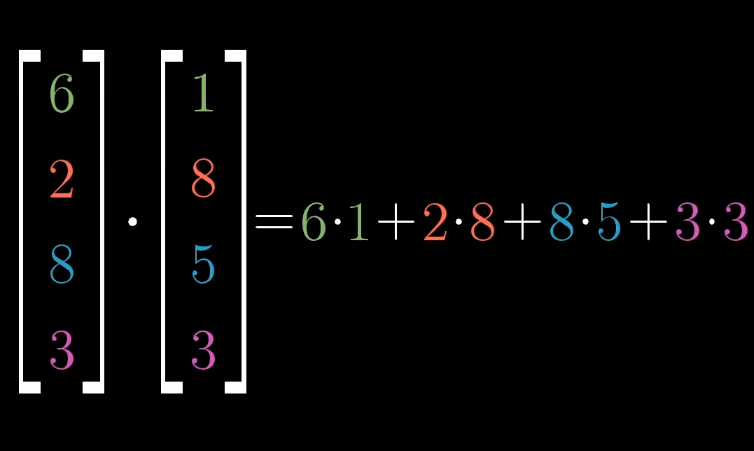
几何直观来说,\(\vec{v} \cdot \vec{w}\) 可以想象成向量 \(\vec{w}\) 朝着过原点和向量 \(\vec{v}\) 的直线上的正交(垂直)投影,然后把投影的长度和向量 \(\vec{v}\) 的长度乘起来就是点积的值。其中正负号代表方向,两个向量成锐角,大于0;钝角,小于0。

点积的顺序
你可能会发现,顺序在线性代数中其实是很重要的,而对于 \(\vec{v} \cdot \vec{w}\) 和 \(\vec{w} \cdot \vec{v}\) 它们的结果是相同的,为什么呢?
解释的方法为:首先假设 \(\vec{v}\) 和 \(\vec{w}\) 长度相同,利用对称轴,两个向量互相的投影相等;接下来如果你缩放其中一个到原来的两倍,对称性被破坏,但是缩放比例没变,最终乘法的结果也没变。
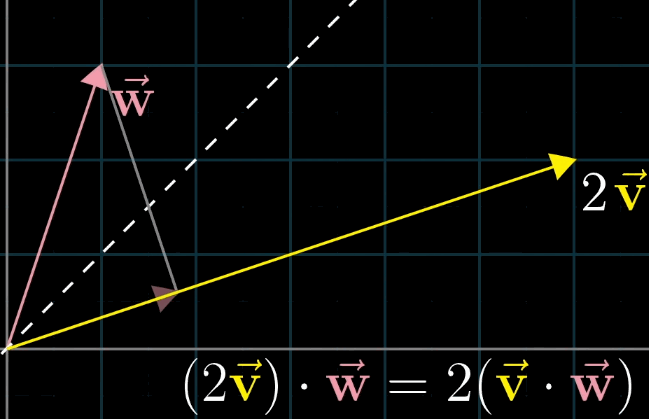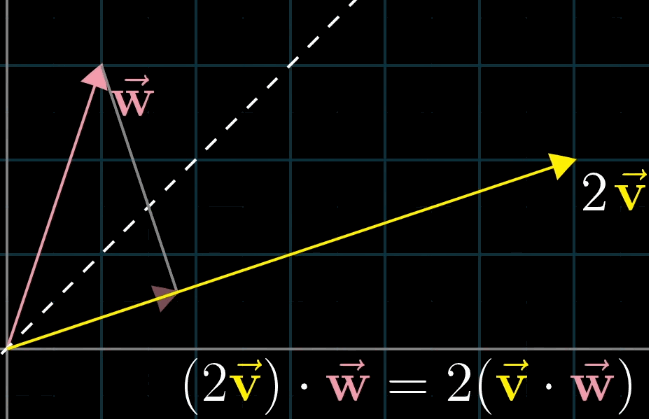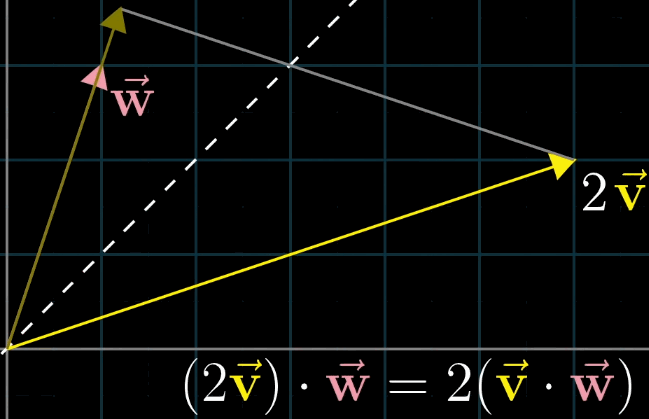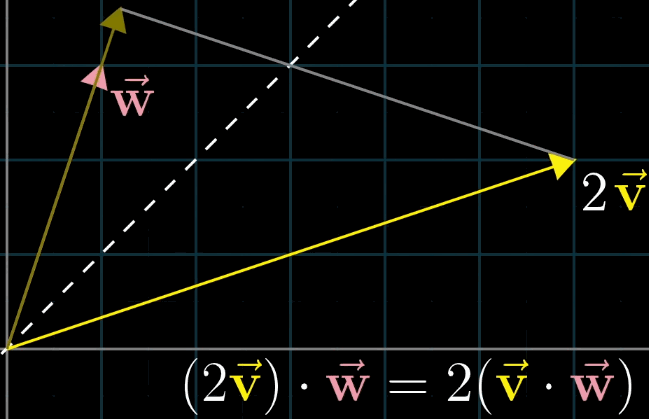
点积与投影
这个时候问题就来了,这种直观的乘法与加法的组合运算:点积为何和投影长度的乘积有关?这个问题非常有意思,因为回答这个问题的过程用到了十分精彩的直觉和思维方式。
首先,需要建立多维空间到一维空间的线性变换(描述为1×n的矩阵,列代表对应的基向量压缩到一维空间的位置),即函数(自变量对应多维空间,\(f(x)\) 最后的输出为一维空间,也就是数轴上的点,一个确定的数)的概念。

你会发现,n×1 表示的是坐标,而1×n表示的多维到一维的变换(矩阵)之间有某种联系,即将向量转化为数的线性变换和这个向量本身有着某种关系。
接下来,我们想象一个情景,这个被压缩成的一条线(数轴)放置在一个坐标系(二维空间)中,且空间所有向量都经过一个变换被压缩到这个数轴上。记这个数轴的单位向量为 \(\vec{u}\)。

这个概念的核心在于理解:任何一个将向量投影到一维空间的线性变换,都可以用点积来表示。这为我们提供了一种全新的理解点积的方式。
再然后,我们需要考虑的问题变为,坐标系中的 \(\hat{\imath}\) 与 \(\hat{\jmath}\) 是如何被压缩到这条直线上的呢(基向量表征整个空间的变换)?即求一个1×2的矩阵内的值,第一列表示 \(\hat{\imath}\) 变换后的位置(在这条数轴上),第二列表示 \(\hat{\jmath}\) 变换后的位置。可以直接给出结论,这个变换的数值恰好就是 \(\vec{u}\) 在这个坐标系中的坐标 \((u_x, u_y)\),推导方法使用到了对称性。
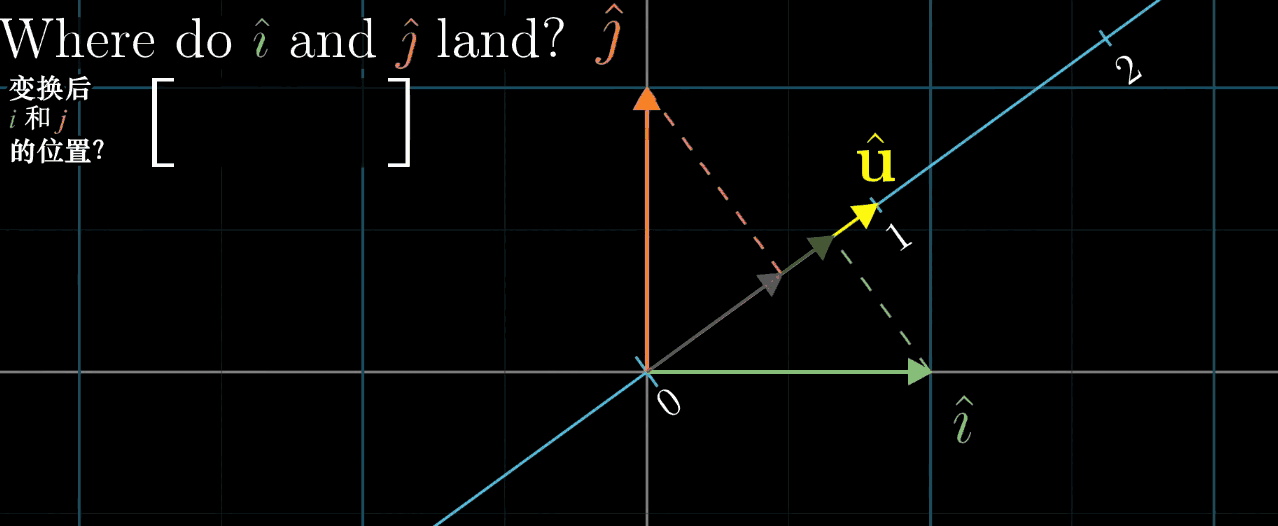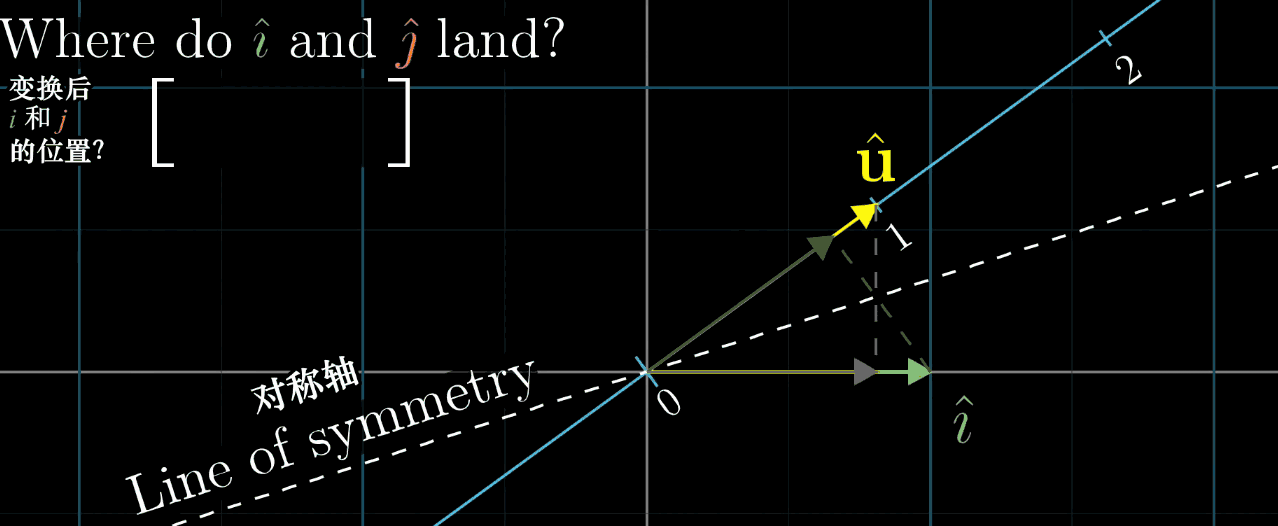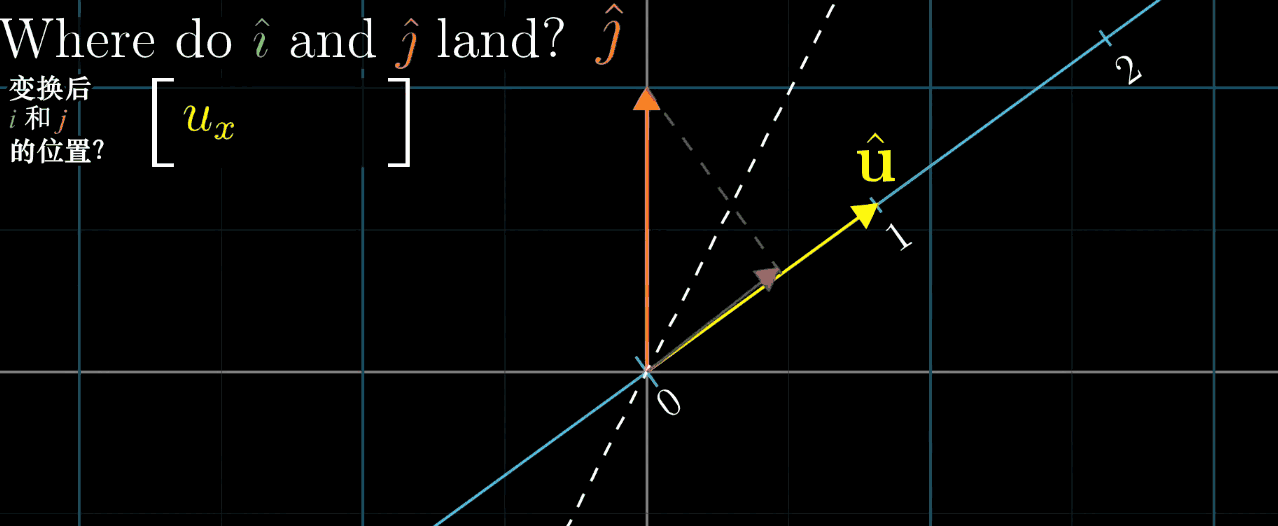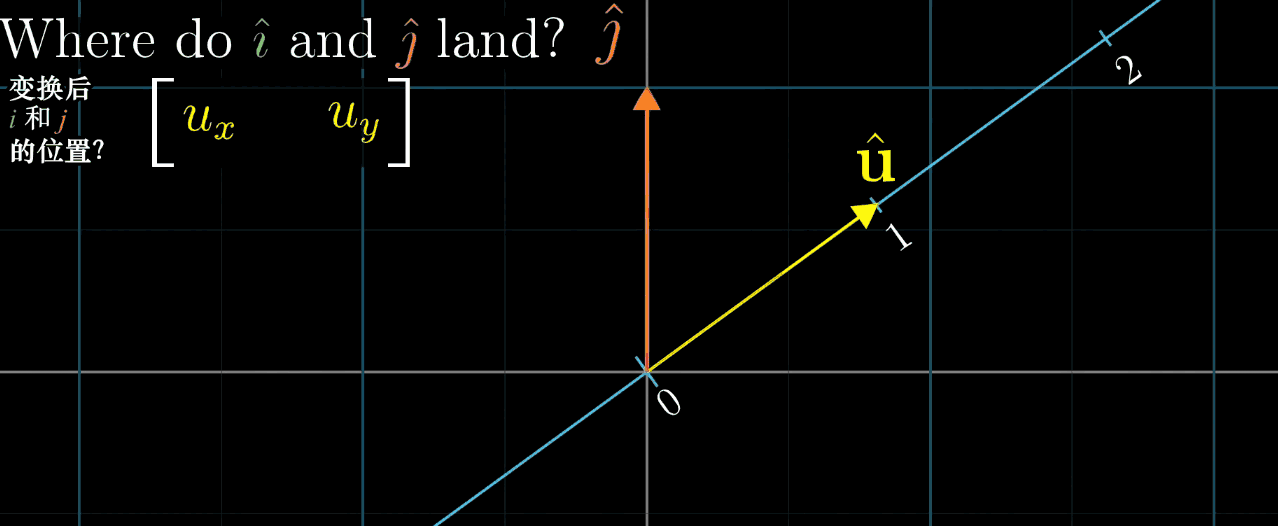
动图中的白色虚线就是对称轴,目的就是确定变换后 \(\hat{\imath}\) 与 \(\hat{\jmath}\) 的位置,即描述变换的矩阵(再次重复,列表示坐标,行表示变换)。
推导完毕,把这个过程总结成一个动图。
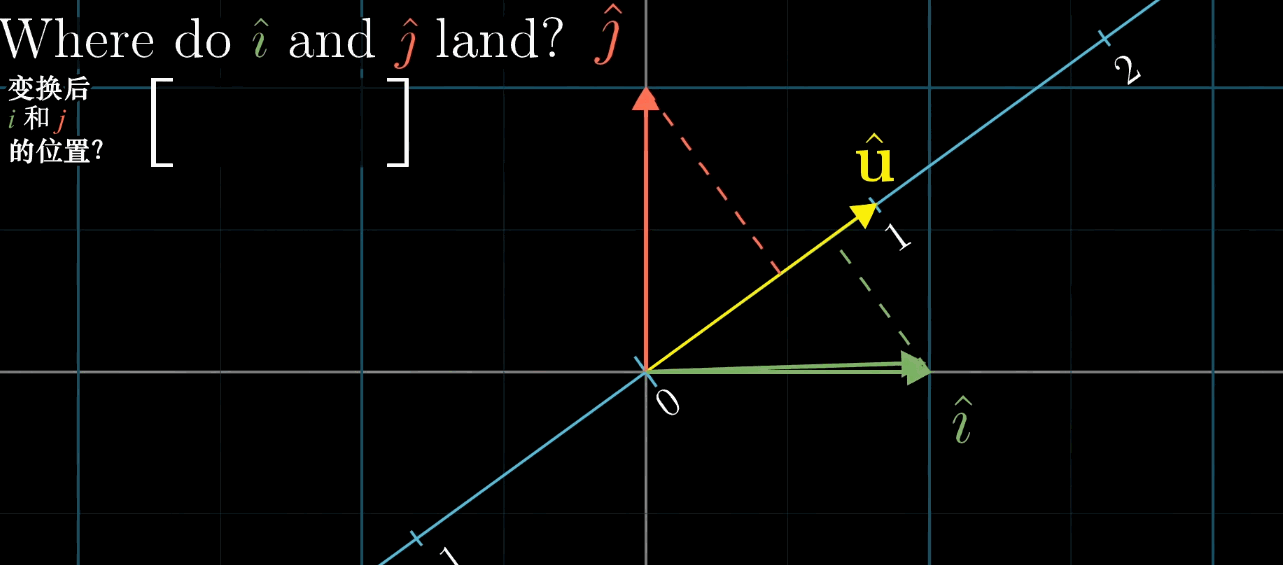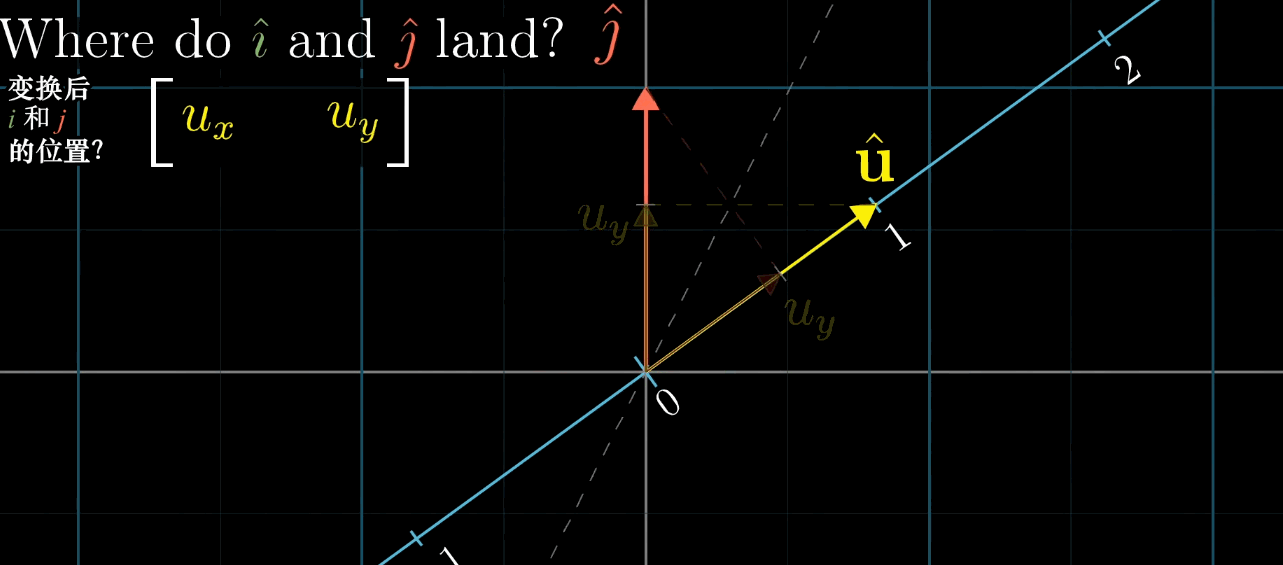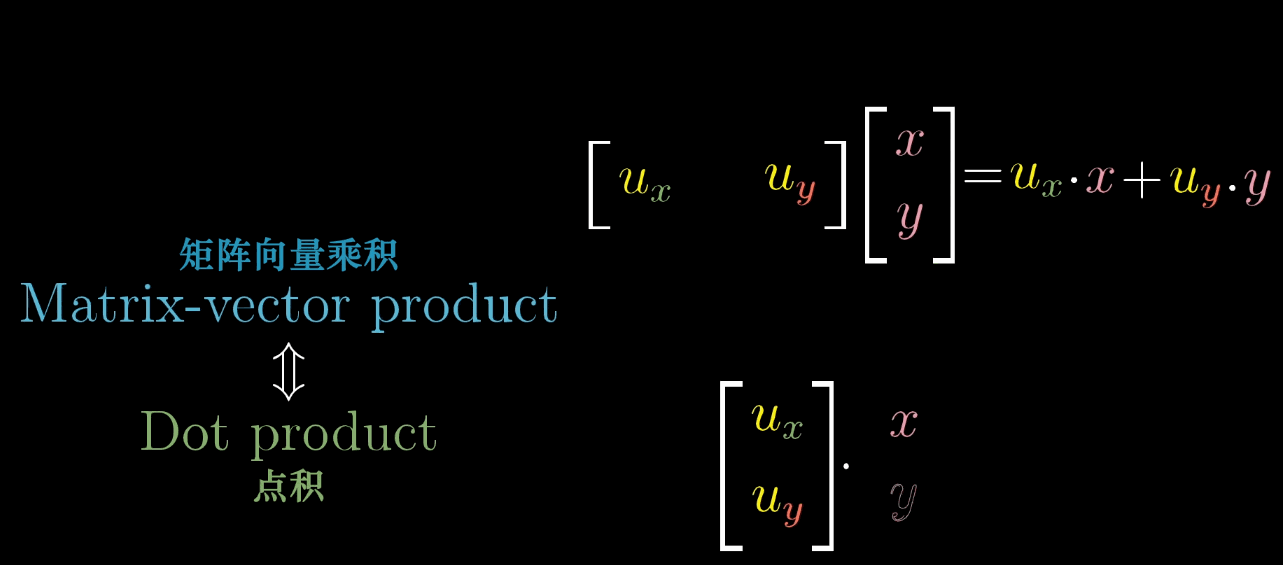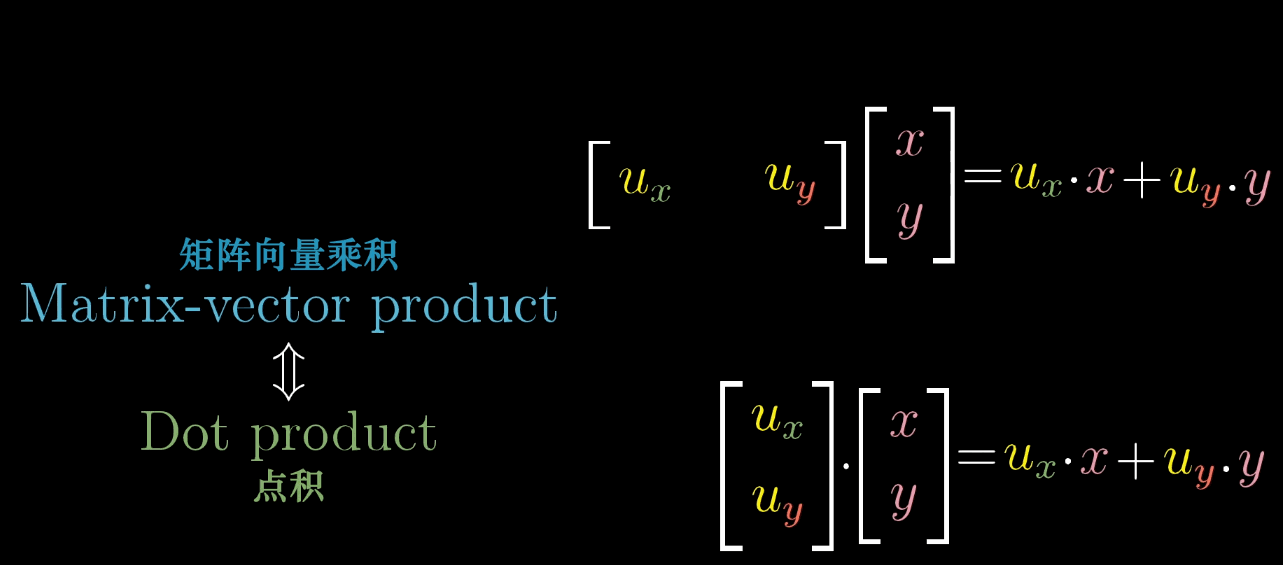
矩阵的向量乘积和点积的计算公式一样,且恰好由压缩这一变换理念,与投影正好联系了起来。关键点,在于压缩变换 = 投影。
这个深刻的联系揭示了线性代数中一个重要的数学原理:对偶性。
对偶性
在证明的过程中,有一个很关键的点就是使用了对称轴(对称理念)。在数学中,对偶性定义为:两种数学事物之间自然而又出乎意料的对应关系。刚刚推导的内容是数学上“对偶性”的一个实例,即无论何时你看到一个二维到一维的变换,空间中会存在一个向量 \(\vec{v}\) 与之相关。
总结
- 点积是理解投影的有力几何工具
- 方便检验两个向量的指向是否相同
- 更进一步,两个向量点乘,就是将其中一个向量转化为线性变换
- 向量仿佛是一个特定变换的概念性记号。对一般人类来说,想象空间中的向量比想象这个空间移动到数轴上更加容易。
通过这种几何直观的理解,点积不再只是一个计算公式,而是变成了一个描述向量间关系的有力工具。这种理解方式将帮助我们在机器学习、物理等领域的应用中更好地运用点积的概念。
叉积
每一个维度都很特别。
从他(格罗滕迪克)和他的作为中,我还学到了一点:不以高难度的证明为傲,因为难度高意味着我们还不理解。理想的情况是能够绘出一幅美景,而其中的证明显而易见。
二维情况下的叉积类比
\(\vec{v}\) 与 \(\vec{w}\) 张成的平行四边形的面积,即 \(\vec{v} \times \vec{w}\),结果方向的确定考虑 \(\hat{\imath}\) 和 \(\hat{\jmath}\) 的相对位置关系,与其相同,为正;否则,为负。
通过这个定义,结合几何直观,我们可以发现几个有趣的结论:
- 越接近垂直的 \(\vec{v}\) 与 \(\vec{w}\) 构成的面积越大。
- 并且叉积的分配律成立。
真正的叉积定义
真正的叉积是在三维情况下被定义出来的:通过两个三维向量(\(\vec{v}\) 与 \(\vec{w}\))产生一个新的三维向量 \(\vec{p}\),向量 \(\vec{p}\) 的长度就是 \(\vec{v}\) 和 \(\vec{w}\) 组成平行四边形的面积,向量的方向与平行四边形(所在平面)垂直,并用右手定则确定方向,食指为 \(\vec{v}\),中指为 \(\vec{w}\),大拇指即 \(\vec{p}\)。
叉积计算公式

其中 \(\hat{\imath}\)、\(\hat{\jmath}\)、\(\hat{k}\) 三个基向量后的数字就是对应向量 \(\vec{p}\) 的坐标值。
第一次学这个计算方法的时候,估计没几个人能想清楚它为什么是这样的形式,甚至老师也说不清,只是告诉学生,我们这么记下来,定义是这样的定义的。但是,既然是直观讲解,必须把这里的来由探明清楚。
叉积计算的几何直观
在开始前,先再次加深一次对偶性的概念:每当你看到一个(多维)空间到数轴(一维空间)的线性变换时,它都与那个空间中的唯一一个向量对应。即应用线性变换到某个向量和与这个向量点乘等价。
恰好,叉积的运算过程给出了对偶性的一个绝佳的实例:根据 \(\vec{v}\) 和 \(\vec{w}\) 定义一个从三维空间到数轴的特定线性变换,找到这个变换的对偶向量,这个对偶向量就是 \(\vec{v}\) 和 \(\vec{w}\) 的叉积。
首先,我们知道三维情况的,求一个3×3矩阵的行列式,就是求这三个向量张成的平行六面体的体积。然后,把第一列(向量)换成一个自变量,后两列(两向量)记为 \(\vec{v}\) 和 \(\vec{w}\),那么我们就有
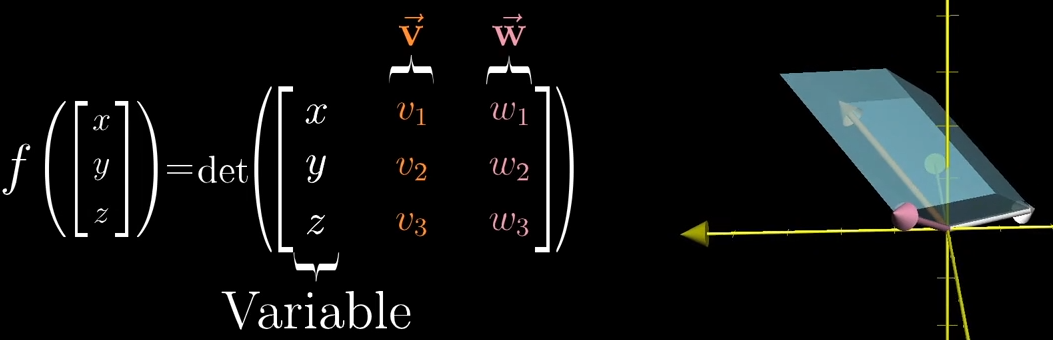
这样形式的函数 \(f()\),如右图所示,即平行六面体随白色向量 \((x, y, z)\) 的随机游走而不断改变。然后,问题就变成了,我们需要根据 \(\vec{v}\) 和 \(\vec{w}\) 找到一个变换(一个矩阵,或者说函数),使得上述等式成立。
并且因为 \(f()\) 是线性的,可以利用对偶性。
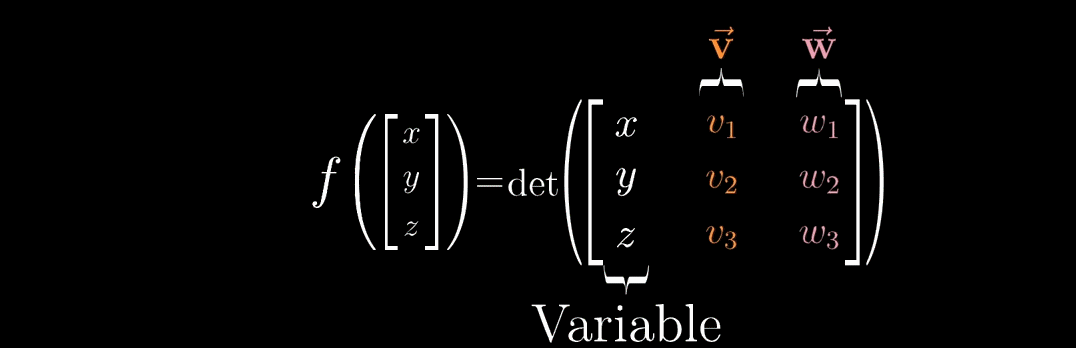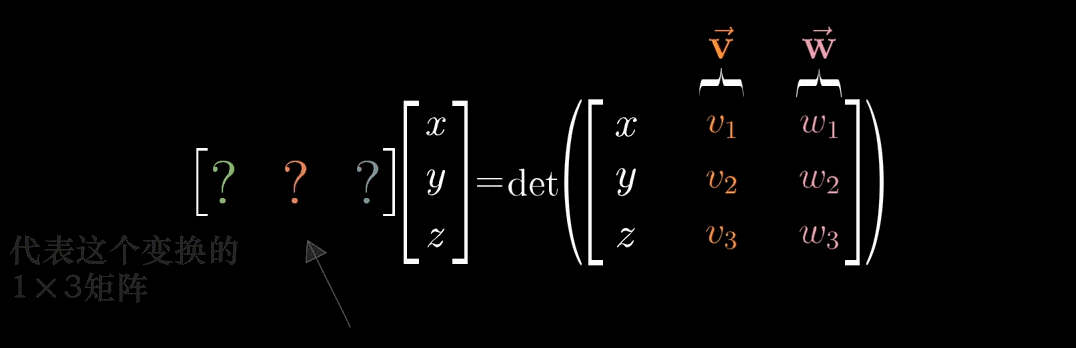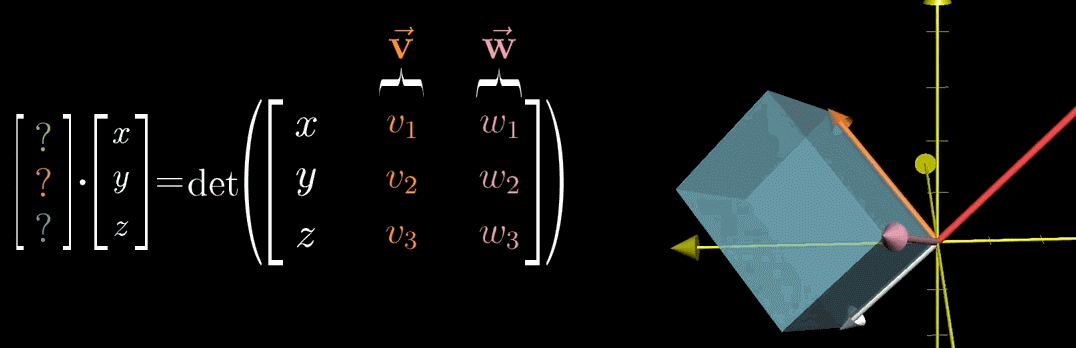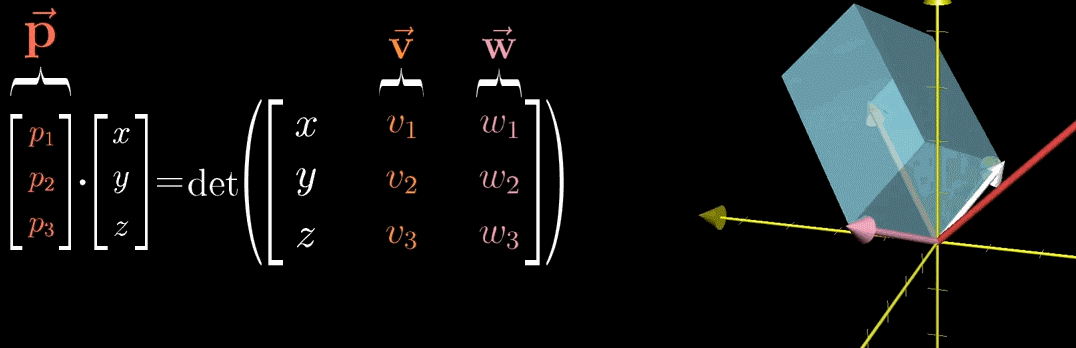
对偶性:即应用线性变换到某个向量和与这个向量点乘等价,即我们可以把1×3的变换(矩阵用来描述变换),立起来(转置),并写成点乘的形式。并把这个向量记为 \(\vec{p}\)。

其中向量的颜色左右对应,并且行列式的值就是右图中平行四面体的体积。然后,我们就把问题进一步变成了:寻找向量 \(\vec{p}\) 使得上述等式成立。
根据点积的性质得知,当你把一个向量与其他向量点积的几何解释是,把其他向量投影到 \(\vec{p}\) 上,然后将投影长度与 \(\vec{p}\) 的长度相乘。而我们知道,对于一个平行六面体来说,体积等于底面积乘以高,高与底面积垂直,所以,作为被投影对象的 \(\vec{p}\) 必须和 \(\vec{v}\) 和 \(\vec{w}\) 构成的平面垂直,方向已经找到。

至于长度,可以看到,一个向量与其他向量点积的几何解释是,把其他向量投影到 \(\vec{p}\) 上,然后将投影长度与 \(\vec{p}\) 的长度相乘,其中投影长度就是 \((x, y, z)\) 向量的长度。根据公式的形式,可以观察得,向量 \(\vec{p}\) 的长度作为第二项,只有当长度等于平行四面体面积时,上述公式(图片中的点积=行列式值的公式)才能成立。
至此,又一次利用对偶性发现了一些事物之间自然而又出乎意料的对应关系。通过几何直观来了解计算公式的由来,也是一种加深印象,深刻理解的有效途径。
总结
在这里总结一下涉及到的过程,也可以通过阅读看看是否直观地理解每句话来判断掌握程度。
- 首先定义了一个三维空间到数轴的线性变换(函数 \(f()\)),它是根据向量 \(\vec{v}\) 和 \(\vec{w}\) 来定义的。
- 接着通过两种不同的方式来考虑这个变换的对偶向量。
- 这种计算方法引导你在第一列中插入 \(\hat{\imath}\)、\(\hat{\jmath}\)、\(\hat{k}\),然后计算行列式。
- 在几何直观上,这个对偶向量一定与 \(\vec{v}\) 和 \(\vec{w}\) 垂直,并且其长度与这两个向量张成的平行四边形的面积相同。
通过这个推导过程,我们不仅得到了叉积的计算公式,更重要的是理解了叉积的几何意义:它是一个同时垂直于两个向量且长度等于它们张成平行四边形面积的向量。
基变换
数学是一门赋予不同事物相同名称的艺术。
Mathematics is the art of giving the same name to different things.
坐标系与基向量
坐标系指:发生在向量与一组数之间的任意转化。如果假设有一个向量,使用 \(\hat{\imath}\) 和 \(\hat{\jmath}\) 来描述是 \(\begin{pmatrix} 3 \\ 2 \end{pmatrix}\),我们把这种描述称为:我们的语言。如果有另一组基向量,\(\hat{\imath}' = \begin{pmatrix} 2 \\ 1 \end{pmatrix}\) 和 \(\hat{\jmath}' = \begin{pmatrix} -1 \\ 1 \end{pmatrix}\)(写成列向量的形式是为了形式上的统一)来描述同样一个向量变成 \(\begin{pmatrix} 5/3 \\ 1/3 \end{pmatrix}\),我们把这种语言记为:詹妮弗的语言。
基变换
我们在之前的解释中已经说明了,在不同的【语言】之间的转化使用矩阵向量乘法。在上面的例子中,转移矩阵是 \(T = \begin{pmatrix} 2 & -1 \\ 1 & 1 \end{pmatrix}\),矩阵的列表示用我们的语言表达詹妮弗的基向量,称为基变换。
反过来,就是求转移矩阵的逆 \(T^{-1}\),称为基变换矩阵的逆,作用是可以表示从詹妮弗的基向量转换回我们的语言需要做的变换。
如何转化一个矩阵
接下来使用一个具体的例子:变换左旋转90°,在我们的语言中,和詹妮弗的语言分别是如何互相转换的来加深印象。
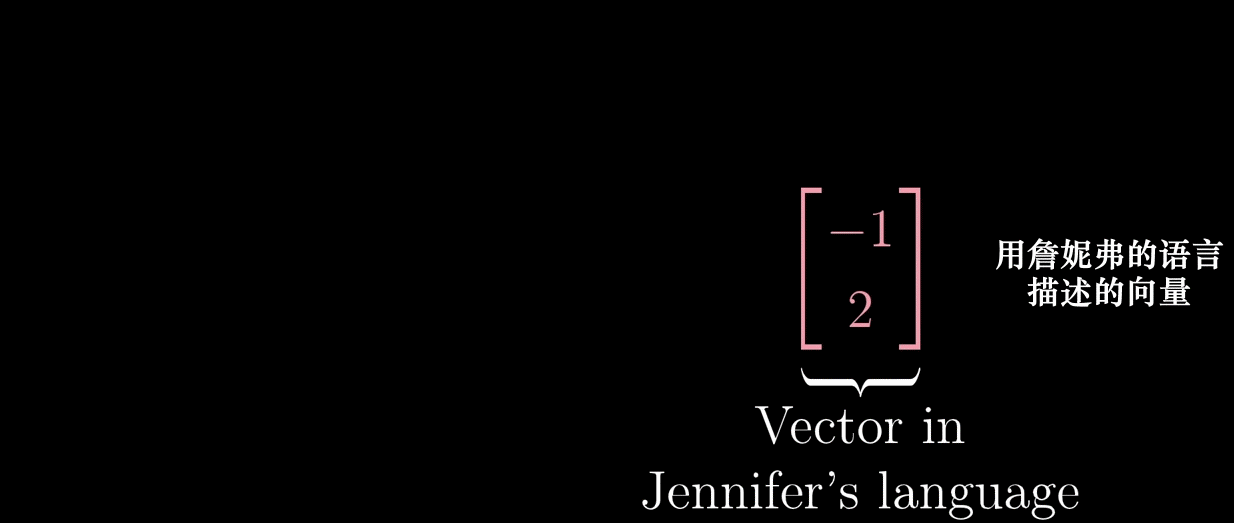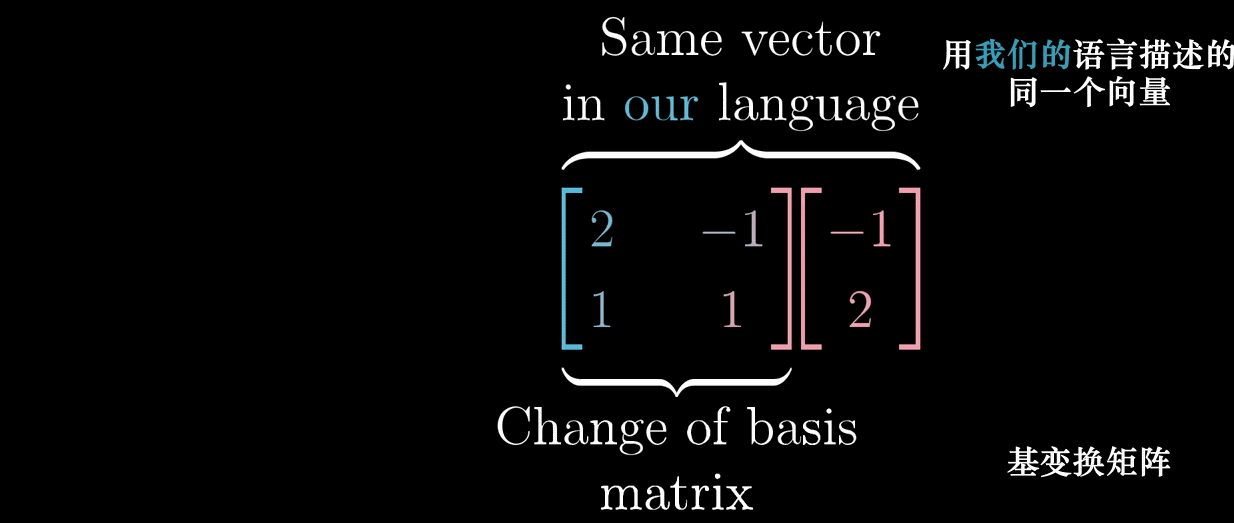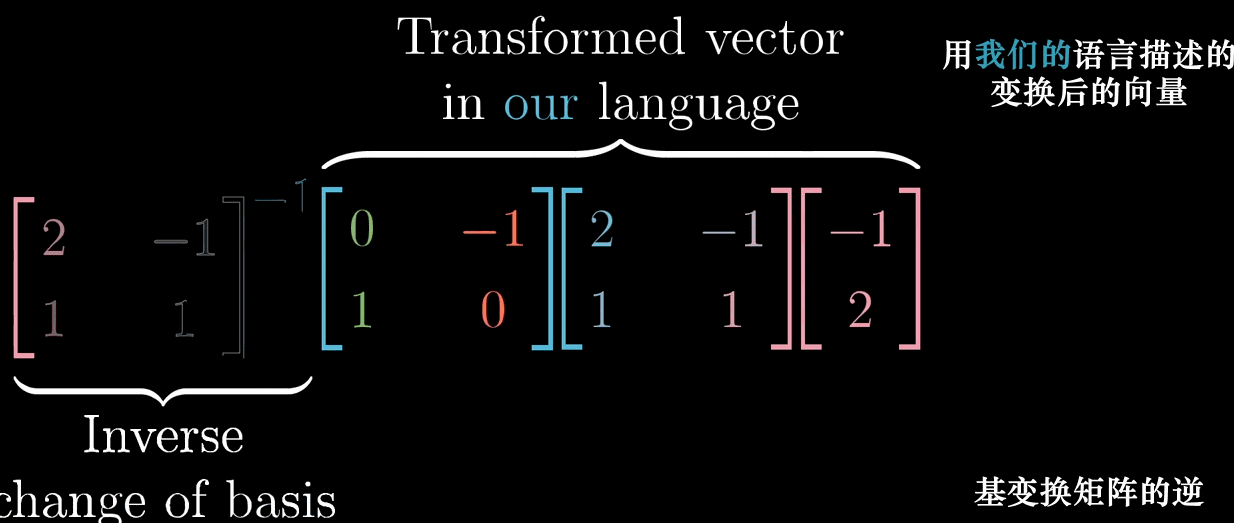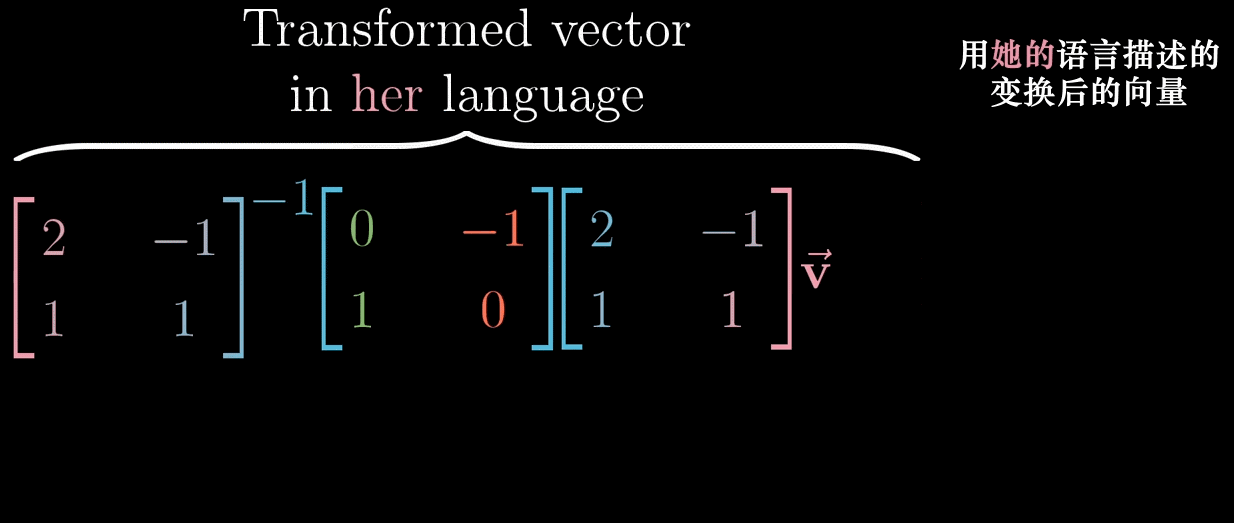
- 左乘基变换矩阵(矩阵的列代表的是用我们的语言描述詹妮弗语言的基向量):需要被转换的詹妮弗的语言:\(\begin{pmatrix} -1 \\ 2 \end{pmatrix}\) ➜ 使用我们的语言描述来描述同一个向量。
- 左乘线性变换矩阵(表示的变化为:左旋转90°):➜ 变换后的向量(还是以我们的语言来描述)。
- 左乘基变换矩阵的逆:➜ 变换后的向量(用詹妮弗的语言来描述)。
这三个矩阵合起来就是用詹妮弗语言描述的一个线性变换。
总结
表达式 \(A^{-1}MA\) 暗示着一种数学上的转移作用。
- 中间的 \(M\) 代表一种你所见的转换(例子中的90°旋转变换)。
- 两侧的矩阵 \(A\) 代表着转移作用(不同坐标系间的基向量转换),即就是视角上的转换。
- 矩阵乘积仍然表示着同一个变换,只不过从其他人的角度来看。
这给了很多域变换的应用一个直观的理解,把这简单的几行记录清晰。
特征向量与特征值
在这一部分中,你会发现,前面提到的所有几何直观:线性变换、行列式、线性方程组、基变换会穿插其中。不仅给了你一个机会检验之前的理解是否深刻(在这一节,会添加一些超链接,方便你进行复习和定位),更多的,现在,是拼装起来感受成就感的时刻了!
What
首先,我们假设坐标系的一个基变换(对 \(\hat{\imath}\) 和 \(\hat{\jmath}\) 张成的空间做一个线性变换),即 \(\hat{\imath}' = \begin{pmatrix} 3 \\ 0 \end{pmatrix}\) 和 \(\hat{\jmath}' = \begin{pmatrix} 1 \\ 2 \end{pmatrix}\)。在变换的过程中,空间内大部分的向量都离开了它所张成的空间(即这个向量原点到终点构成的直线),还有一部分向量留在了它所张成的空间,矩阵对它仅仅是拉伸或者压缩而已,如同一个标量。
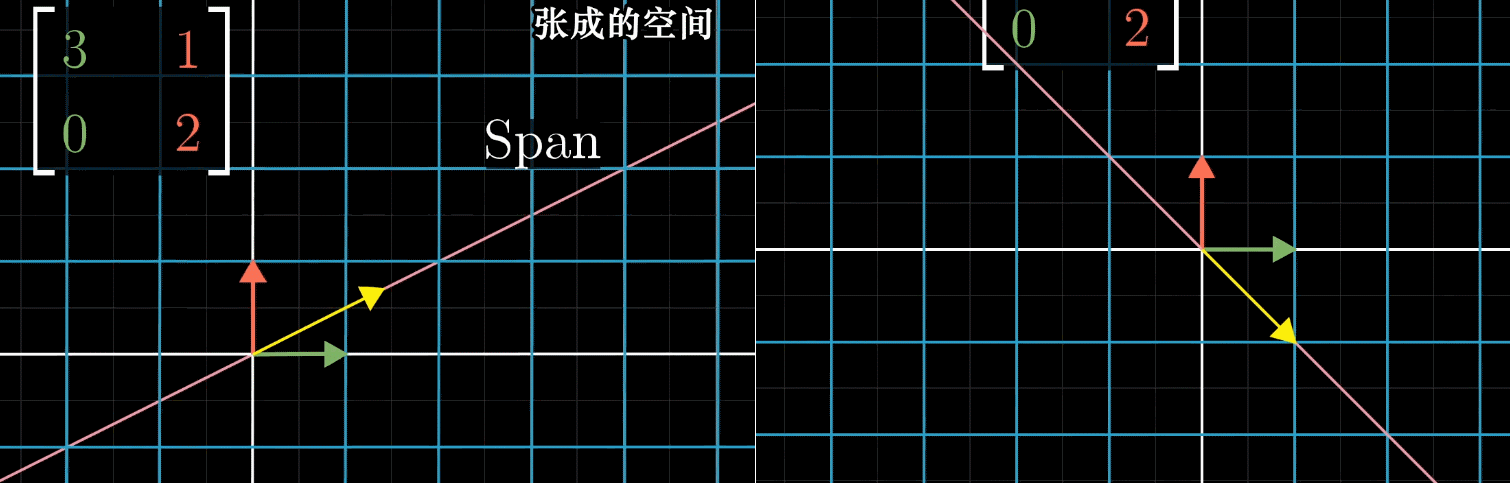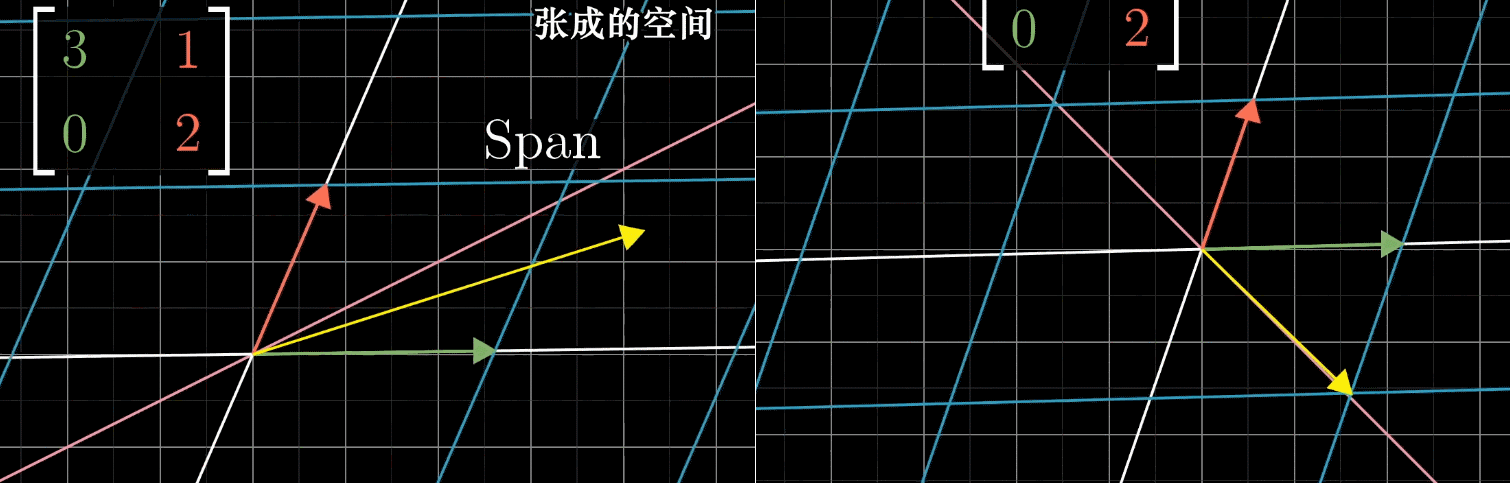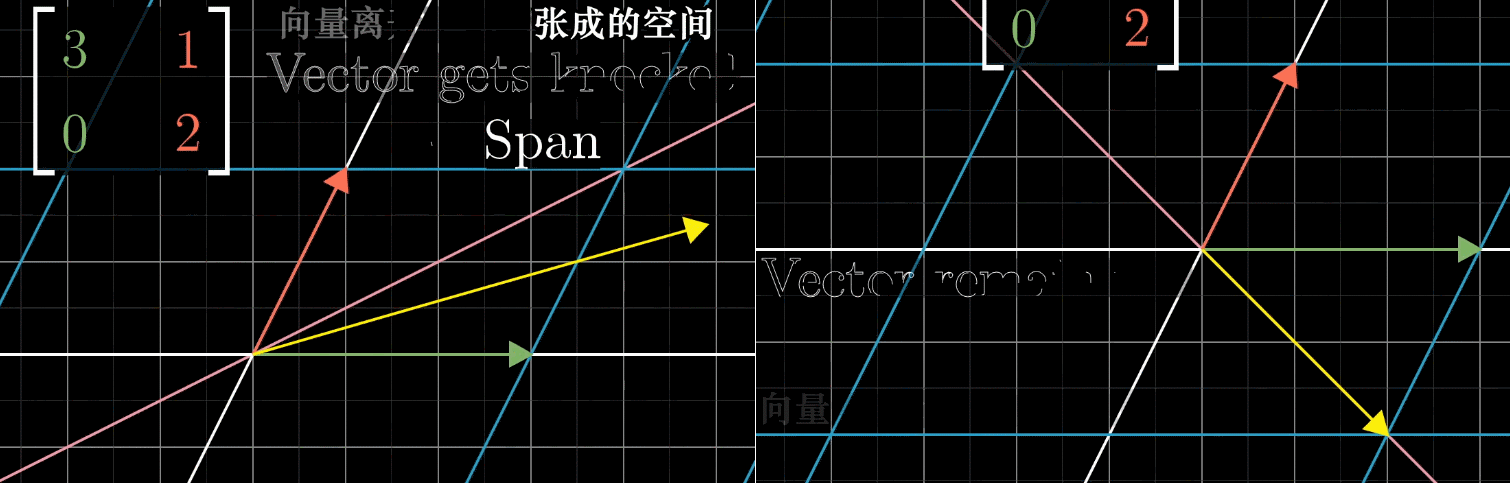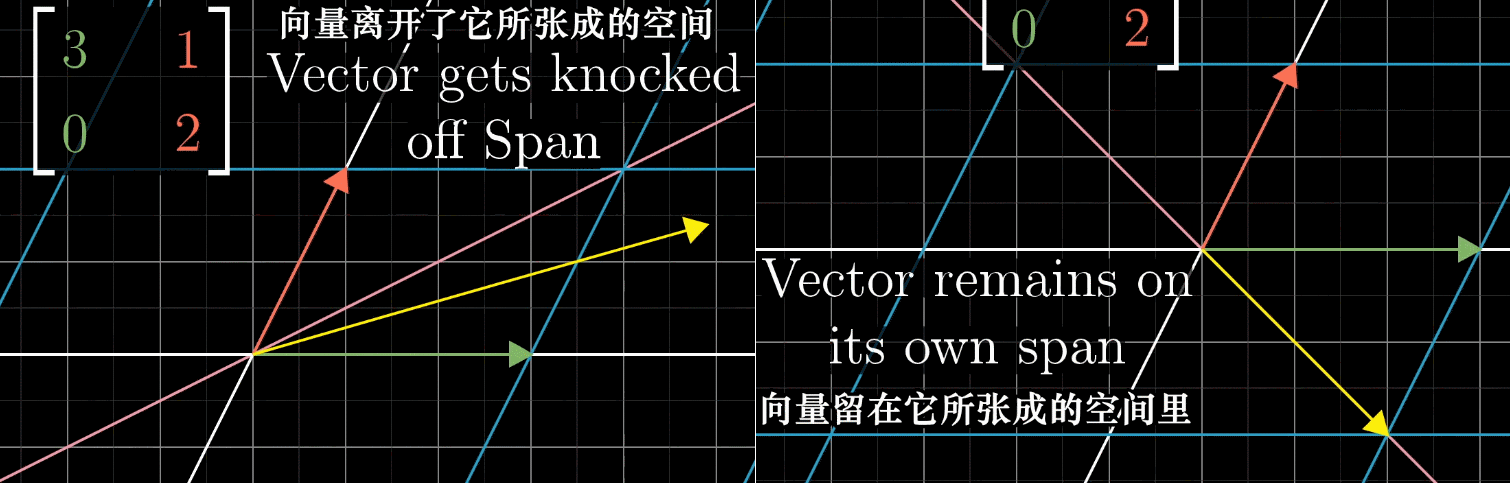
如上图,是给出例子中,x轴所有向量被伸长为原来的3倍,一个明显留在张成空间内的例子。另一个比较隐藏的,是\((-1,1)\)这个向量,其中的任意一个向量被伸长为原来的2倍。
- 变换中被留在张成空间内的向量,就是特征向量(上例x轴和\((-1,1)\))。
- 其中每个向量被拉伸或压缩的比例因子,就是特征值(上例3和2)。
- 正负表示变换的过程中是否切翻转了方向。
特征向量和特征值的本质就是:在线性变换中保持方向不变(或仅反向)的特殊向量及其缩放比例。
Why
三维情况,如果能找到这个不变的向量,即旋转轴(特征值必须为1)。
理解线性变换的作用的关键(或者说更好的描述一个变换),更好的方法是求出它的特征向量和特征值。
特征向量和特征值的重要性在于:
- 它们揭示了线性变换的本质特性
- 它们提供了一种简化的视角来理解复杂变换
- 在许多实际应用中(如主成分分析、振动分析等),特征向量和特征值具有明确的物理意义
How
从计算角度来看特征值和特征向量,里面包含了很多对以前知识的回顾和整合。
根据特征向量和特征值的定义,使用数学的方法来表示即
\[ A\vec{v} = \lambda\vec{v} \]
\(A\) 是求特征值和特征向量的变换矩阵;\(\vec{v}\) 是特征向量;\(\lambda\) 是特征值;目标是找 \(\vec{v}\) 和 \(\lambda\)。
至于为何会用这个式子来定义特征向量和特征值呢,我们继续观察这个式子中的 \(\lambda\vec{v}\),考虑到右边是一个矩阵乘法,我们希望左右都是一个矩阵乘法,这样方便等价和计算。观察发现,\(\lambda\vec{v}\) 就是给 \(\vec{v}\) 中每一个元素都乘以 \(\lambda\)。对角矩阵 \(I\) 且对角线元素为 \(\lambda\) 的矩阵也能有同样的变换结果,得到下列表达式
\[ A\vec{v} = (\lambda I)\vec{v} \implies (A - \lambda I)\vec{v} = 0 \]
观察这个等式你会发现:可以把 \(A - \lambda I\) 矩阵看成一个对 \(\vec{v}\) 的变换,目的是把 \(\vec{v}\) 压缩到更低的维度。而空间压缩对应的恰好就是变换矩阵的行列式为0(期待你在品读这句话的时候感受到满满的成就感,实在有难度,再结合下图)。
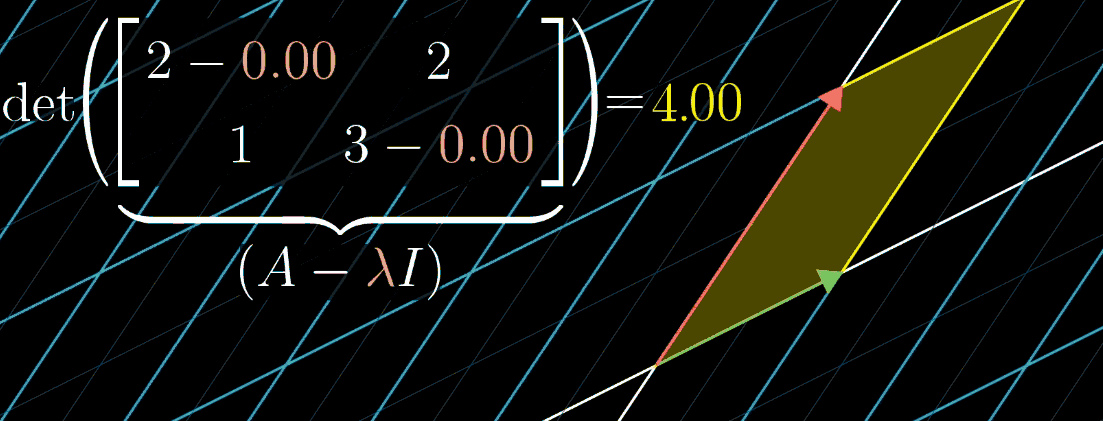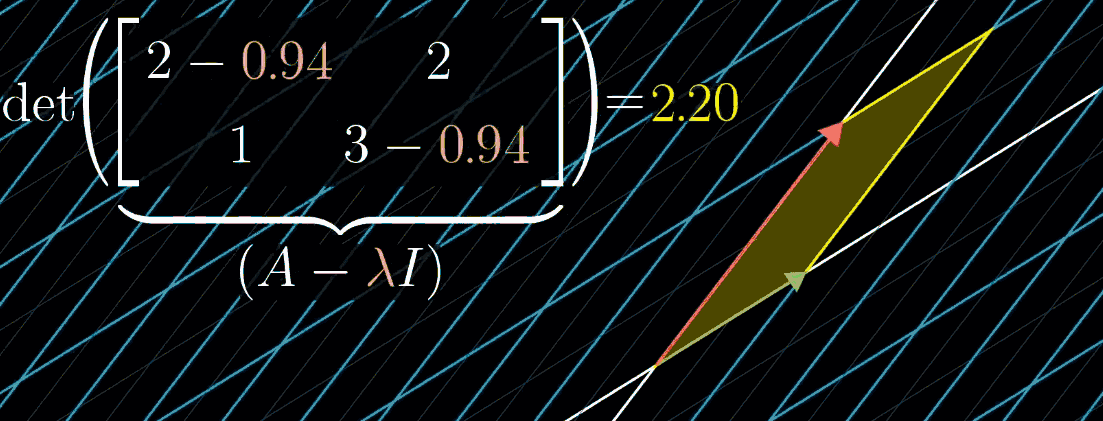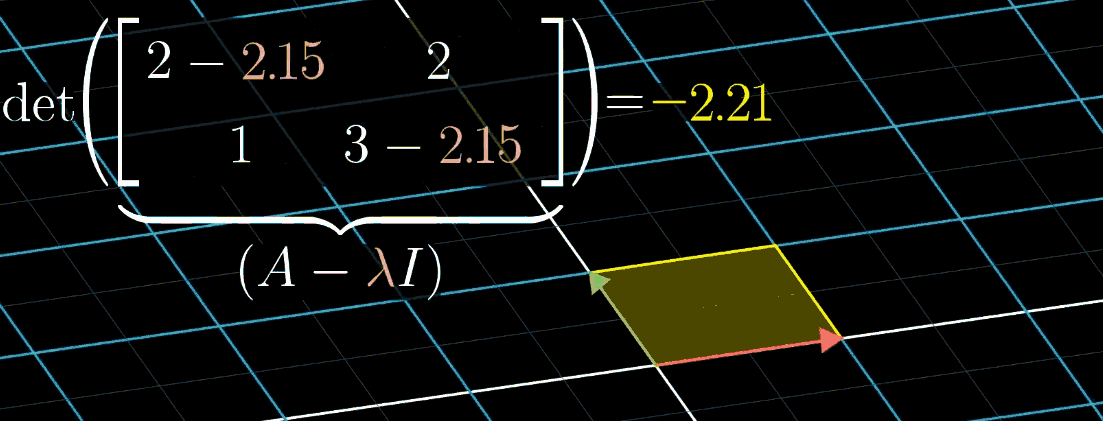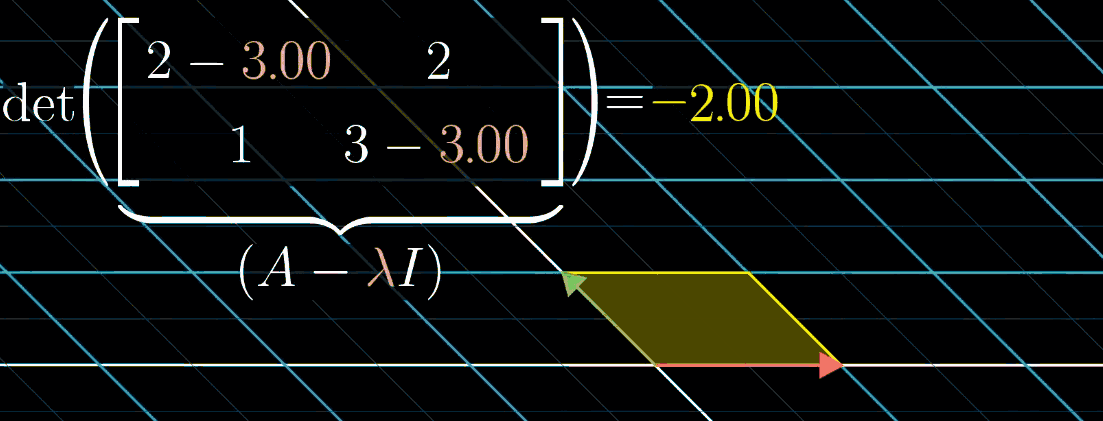
上图显示随 \(\lambda\) 可视化的变化情况,从这幅图中,使用的例子是 \(\begin{pmatrix} 2 & 2 \\ 1 & 3 \end{pmatrix}\),特征值恰好是1。
特征向量的特殊情况
旋转变换
解出特征值能发现答案是 \(\pm i\),没有特征向量存在,即特征值出现复数的情况一般对应于变换中的某种旋转。这说明纯旋转变换没有保持方向不变的向量。
剪切变换
Shear变换。x轴不变,只有一个特征值,为1(\((\lambda - 1)^2 = 0\))。这种变换虽然改变了大部分向量的方向,但保持了x轴上的向量不变。
伸缩变换
特征值只有一个,但是是空间中所有的向量都是特征向量。这种变换将所有向量都沿着相同的方向拉伸或压缩相同的倍数。
特征基
对角矩阵:只有对角线非零的矩阵。解读它的方法是:所有的基向量都是特征向量。因为之前提到过,矩阵的第一列是 \(\hat{\imath}\),第二列是 \(\hat{\jmath}\),往后同理。这样就能发现,如果一列只有对应的位置非零,那么这个坐标轴本身就是一个特征向量。
一组基向量(同样是特征向量)构成的集合被称为一组:特征基。
对角矩阵有一个好处是计算方便,多次矩阵乘法非常容易。
这时我们就希望利用对角矩阵(基向量为特征向量)的便于计算的特性,利用上一节提到的基向量变换的方法,把特征向量作为基,对每一个矩阵进行变换后再进行计算,最后再左乘变换矩阵的逆求回原矩阵得到结果,如下图所示。
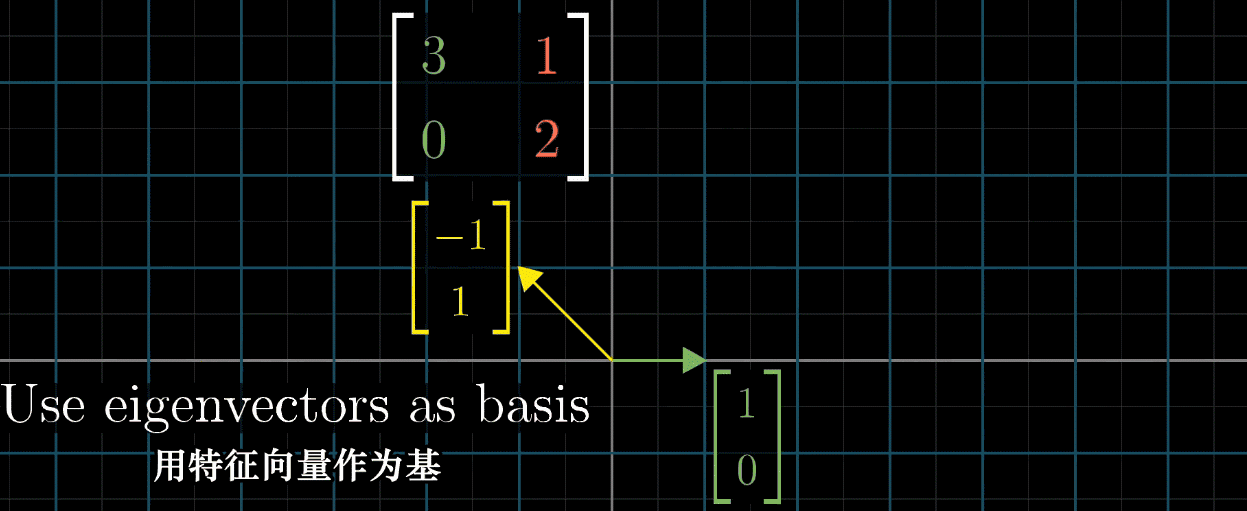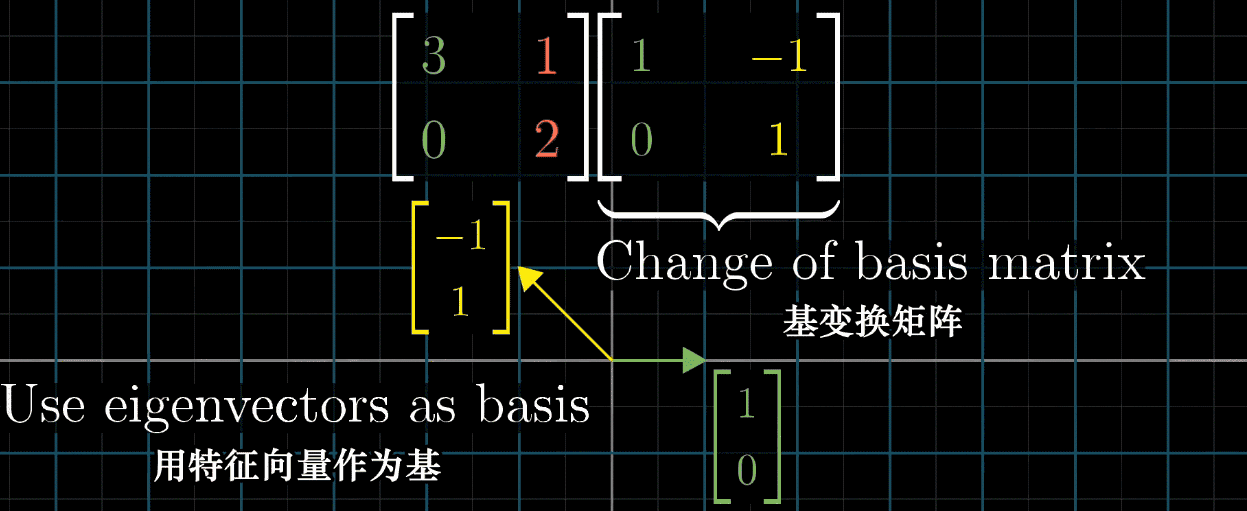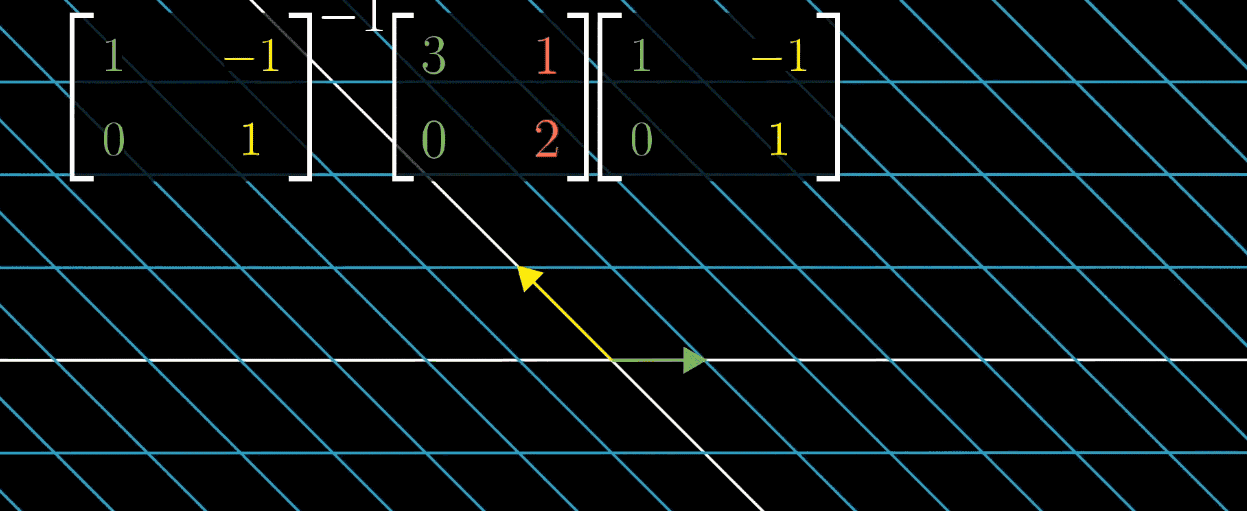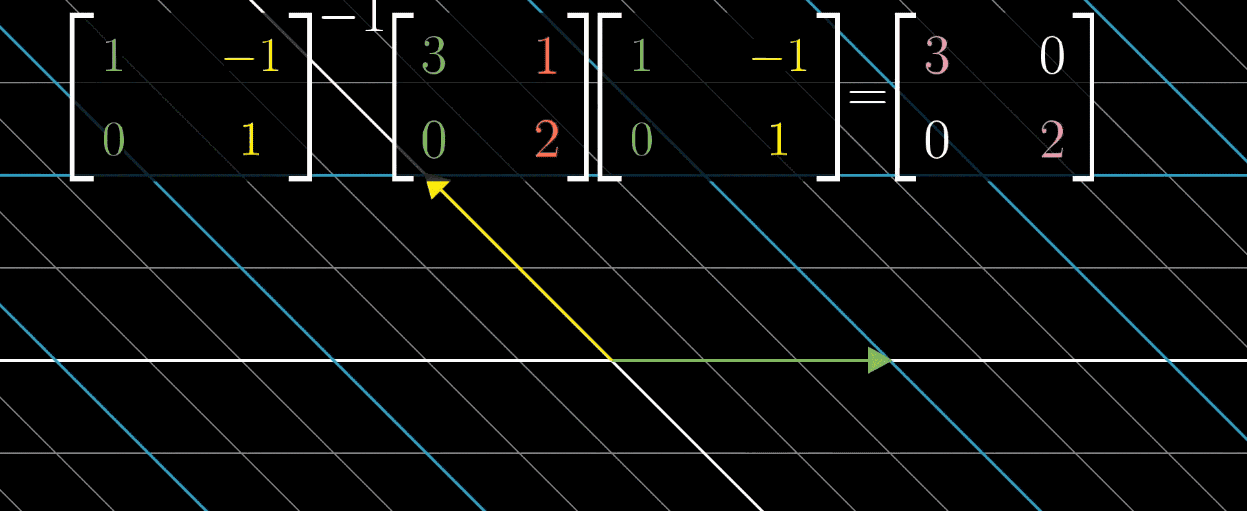
但需要说明的是,并不是所有的矩阵都能对角化,比如Shear变换,它的特征向量不够多,不足以张成一个空间。这种情况下的矩阵被称为缺陷矩阵,它们无法通过简单的对角化来简化计算。
抽象向量空间
线性代数的一切概念,如行列式和特征向量,它们并不受所选坐标系的影响,但是这两者是暗含于空间中的性质。
这里所说的空间是什么意思呢?
函数与向量
从某种意义上来说,函数实际上也只是另一种向量。对于函数来说,也有可加性、可比性。
\[ (f + g)(x) = f(x) + g(x) \\ (2f)(x) = 2f(x) \]
你能发现,这两个性质和向量加法与数乘是息息相关的。所以我们对于矩阵中所有定义的概念和方法,都可以相对应地应用到函数中。如函数的线性变换:函数接受一个函数,并把它变成另一个函数。如微积分中可以找到一个形象的例子——导数。关于这一点,你听到的可能是【算子】,而不是【变换】,但他们所要表达的思想是一样的。
以导数为例,既然两者是一个东西,那么我们可不可以使用矩阵来描述多项式空间呢?
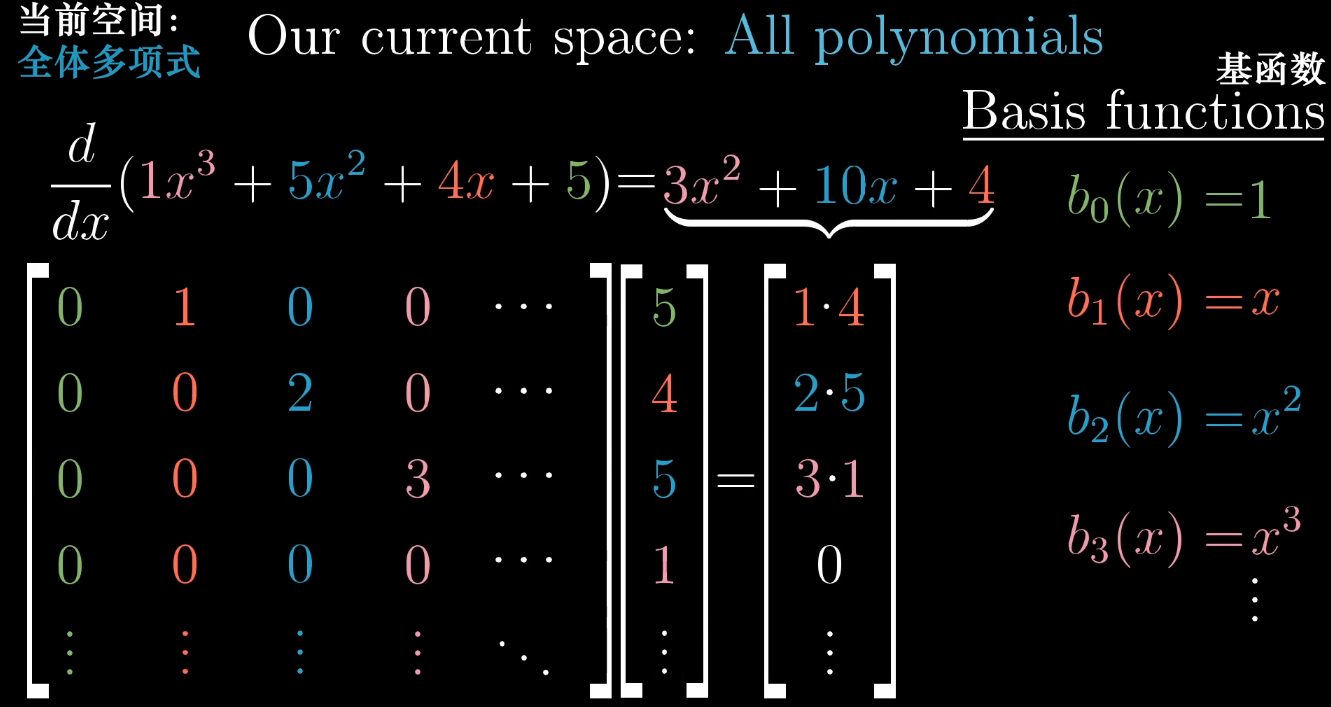
如上图,以取 \(x\) 的不同幂次方作为基函数,然后既可以写出求导变换的矩阵。这更进一步佐证了开篇提到的关键句子,矩阵 = 变换的数字表达。
| 线性代数 | 函数 |
|---|---|
| 线性变换 | 线性算子 |
| 点积 | 内积 |
| 特征向量 | 特征函数 |
如上表一样,相同的概念只是在不同的领域有着不同的名称罢了。
有很多类似向量的不同事物,只要你处理的对象具有合理的数乘和相加的概念,线性代数中所有关于向量、线性变换和其他的概念都应该使用于它。作为数学家,你可能希望你发现的规律不只对一个特殊情况适用,对其他类似向量的事物都有普适性。
向量空间
这些类似向量的事物,比如箭头、一组数、函数等,他们构成的集合被称为:向量空间。
向量加法和向量数乘的规则 - 被称为公理,如下图。

它仅仅是一个待查列表,以保证向量加法和数乘的概念确实是你所希望的那样。这些公理是一种媒介,用来连接数学家和所有想要把这些结论应用于新的向量空间的人。
仅仅根据这些公理描述一个空间,而不是集中于某一个特定的向量上。简而言之,这就是为什么你阅读的每一本教科书都会根据可加性和成比例来定义线性变换。
总结
对于【向量是什么】这个问题,数学家会直接忽略不作答。向量的形式并不重要,只要相加和数乘的概念遵守八条公理即可。就和问“3”究竟是什么一样。在数学中,他被看作是所有三个东西的集合的抽象概念,从而让你用一个概念就能推导出所有三个东西的集合。向量也是如此,它有很多种体现,但是数学把它抽象成【向量空间】这样一个无形(抽象)的概念。
普适的代价是抽象(abstractness is the price of generality)。学习的过程只能来源于解决问题,来源于带有思考的不断重复,但如果你具备了正确的直观,你会在以后的学习中更加高效。