线性代数的本质(更新中)
序言
There is hardly any theory which is more elementary than linear algebra, in spite of the fact that generations of professors and textbook writers have obscured its simplicity by preposterous calculations with matrices.
尽管一批教授和教科书作者用关于矩阵的荒谬计算掩盖了线性代数的简明性,但鲜有比之更基本的理论。
将只停留在数值运算和公式的线性代数与可视化几何直观(Visual Geometric Intuition)结合,整理自3Blue1Brown的系列视频。内容涉及到向量,线性变换,行列式,逆矩阵,点积与叉积,特征向量与特征值等,以及二次型,相似矩阵等补充内容。

我们为什么需要几何直观
在开始之前,想象学习一个事物(概念)的场景:我们需要学习正弦函数 $\sin (x)$ ,非常不幸的是,你遇到的教材告诉你,正弦函数是这样的:
$\sin (x) = x - \frac{x^3}{3!} + \frac{x^5}{5!} + \cdots + (-1)^n\frac{x^{2n+1}}{(2n+1)!} + \cdots$
看上去很厉害的样子,并且计算机也的确是这么计算 $\sin (x)$ 的,而对你来说,计算$\sin (\frac{\pi}{6})$可能就是把 $x= \frac{\pi}{6}$ 代入公式,然后神奇的发现结果越算越接近0.5 ,此时你对$\sin (x)$与三角形之间的几何直观只有一些模糊的概念,这样的学习就十分悲催了。为什么呢?再假设一个场景:
在学完$\sin (x)$函数后,你又去参加了一个物理课程,正弦函数随处可见,其他人很快就能知道如何使用它并能得出大概值,而刚学完正弦函数的你内心戏大概是这样的:这群学物理的脑子也太强了!
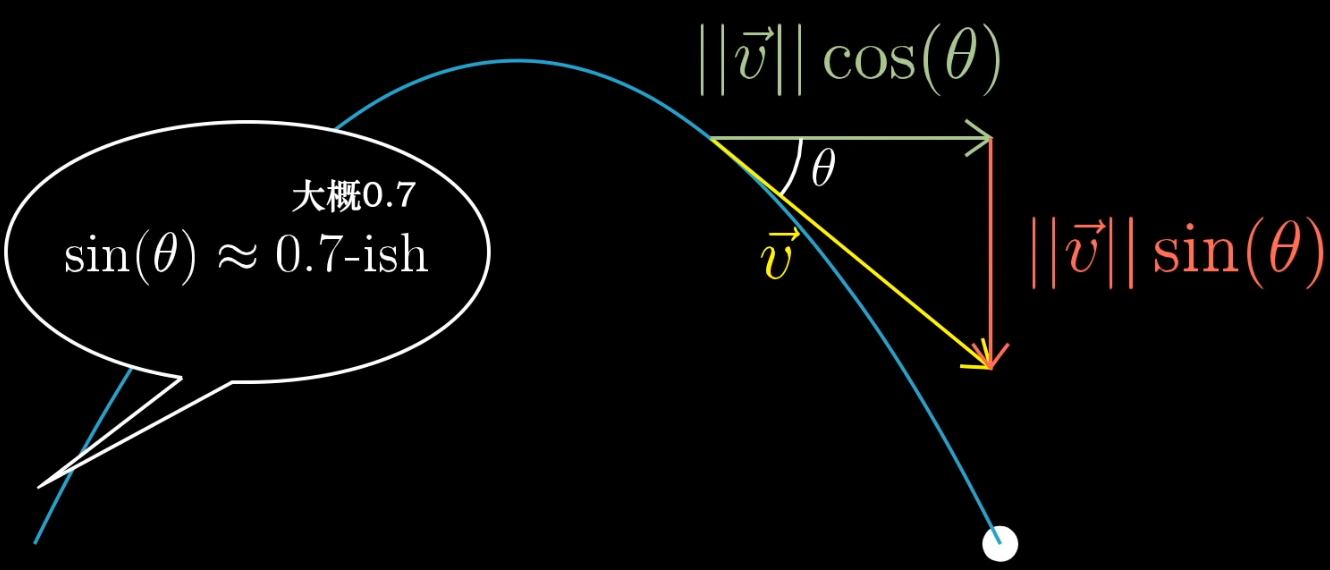
其实,你需要只是一个几何直观的灌输而已,这也从侧面佐证了一个好的老师或教材(这里的好老师真的不是他本身的学术能力有多强,而在于他擅不擅长站在学习者的角度不断的修正教学方法)是有多么重要。
教学不同层次的人:初学、入门、掌握、理解,解释的角度,方式都完全不同。更加不幸的是,为了能更加通用的用理论来描述现实生活中的规律,人类已经做了很多工作,我们常说:越通用,越抽象,这对于初学者来说堪称一段噩梦。
上述例子可能比较极端,但只为强调一件事:直观理解很重要,或者说,学习方法很重要。好的学习方法即你如何直观的去理解(可能是几何的,或是现实中的具体例子)一个抽象的事物,并层次化的建立知识与知识间的联系,构建并健壮属于自己的知识图谱。个人观点是,这种学习方法是最高效的。它唯一的要求在于,需要一定的基础知识打底,一定的量变结合方法论(点拨或领悟)就是质变。
向量究竟是什么
The introduction of numbers as coordinates is an act of violence.
引入一些数作为坐标是一种鲁莽的行为。
不同视角下的向量
对于向量的这个概念,大家一定并不陌生,但是这次让我们从数学,物理,计算机三个角度来看待如何定义这个向量这个概念。
物理专业角度
- 向量是空间中的箭头
- 决定一个向量的是:它的长度和它所指的方向
计算机专业角度
- 向量是有序的数字列表
- 向量不过是“列表”一个花哨的说法
- 向量的维度等于“列表”的长度
数学专业角度
对数学来说,它的本质就是通用和抽象,所以,数学家希望概括这两种观点:
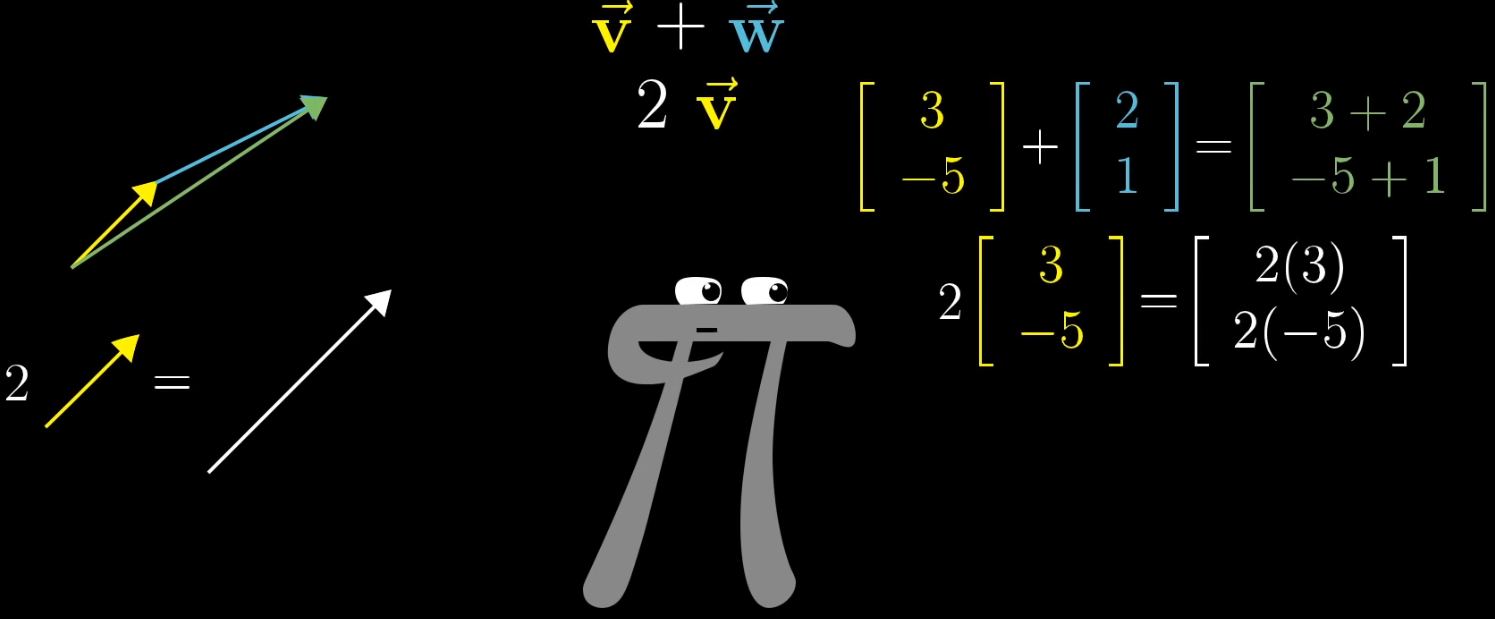
- 向量可以是任何东西,只需要保证:两个向量相加及数字与向量相乘有意义
- 向量加法和向量乘法贯穿线性代数始终,十分重要
可以通过上图直观的感受到数学家在想什么。左边是物理角度,右边是计算机角度,但是很抱歉,我能用一些抽象的定义和约束让你们变成一个东西。
坐标系
把向量置于坐标系中,以原点为起点,坐标正负表示方向,可完美把两个不同的角度融合。
- 向量加法
- 物理:首尾相连 (Motion)
- 计算机:坐标相加
- 向量乘法
- 物理:缩放 (Scaling)
- 计算机:坐标和比例相乘
实际上无论你怎么看待向量都无所谓,或把向量看作空间中的箭头,或把向量看作数字列表,线性代数的效用很少体现在这些观点中的其中一个上,而是更多的体现在它能够在这些观点中互相转化。线性代数为数据分析提供了一条将大量数据列表概念化、可视化的渠道,它能让数据样式变得非常明晰,并让你大致了解其特定运算的意义。同时,线性代数给物理学家和计算机图形程序员提供了一种方法去通过计算机能处理的数字来描述并操纵空间(例如Mathematical Animation Engine)。
线性组合、基与其张成的空间
Mathematics requires a small dose, not of genius, but of an imaginative freedom which, in a larger dose, would be insanity.
数学需要的不是天赋,而是少量的自由想象,但想象太过自由又会陷入疯狂。
本部分继续加深一个概念,为何向量加法与向量乘法是那么重要,并从始至终贯穿整个线性代数(关于后面的直观解释部分,强烈建议去原视频观看动画演示)。
线性组合
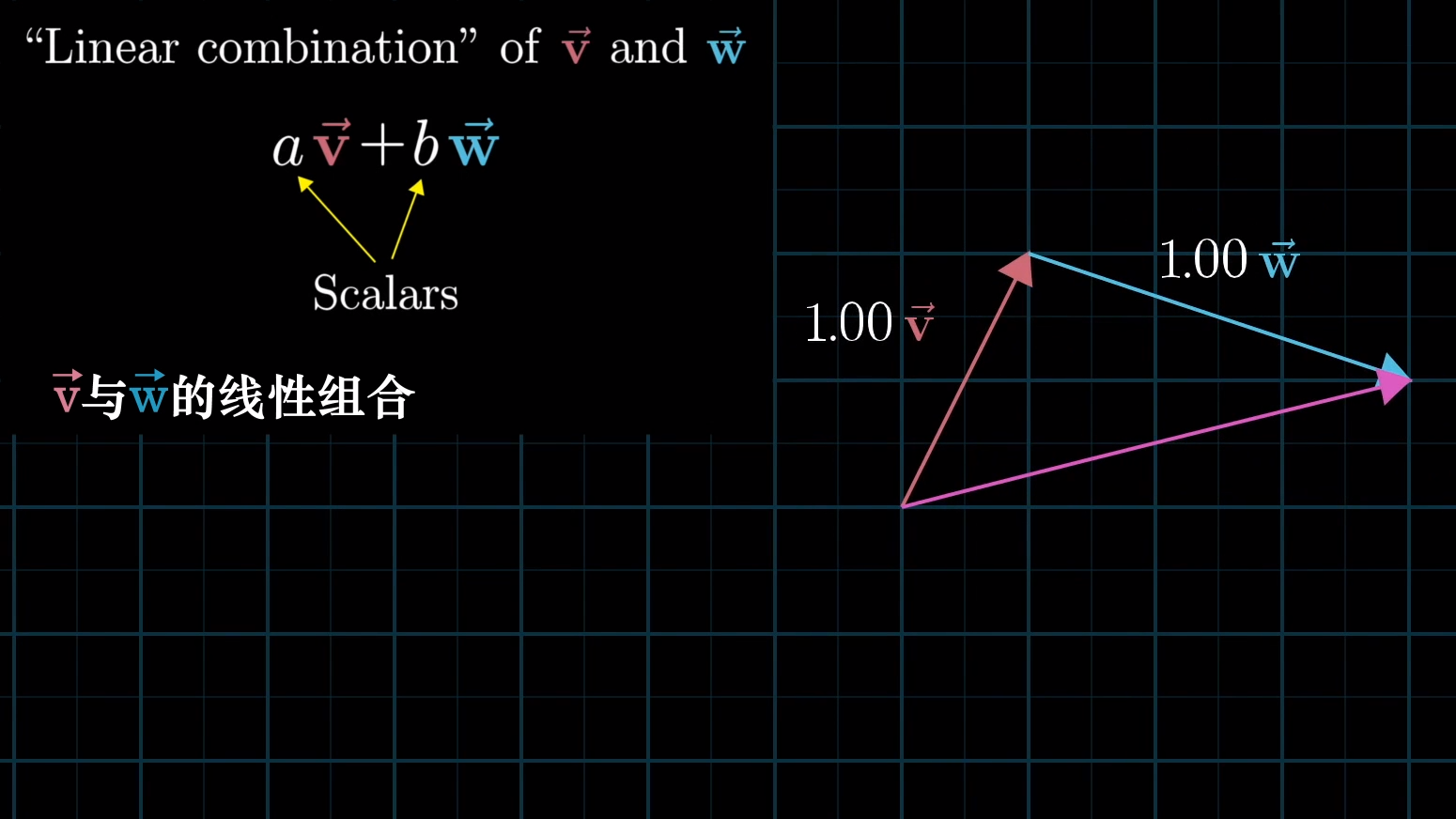
二维空间中任意两个不共线的非零向量都可以表示该空间中的任意一个向量,写成符号语言就是: $a \mathbf{\vec v} + b \mathbf{\vec w}$ 。
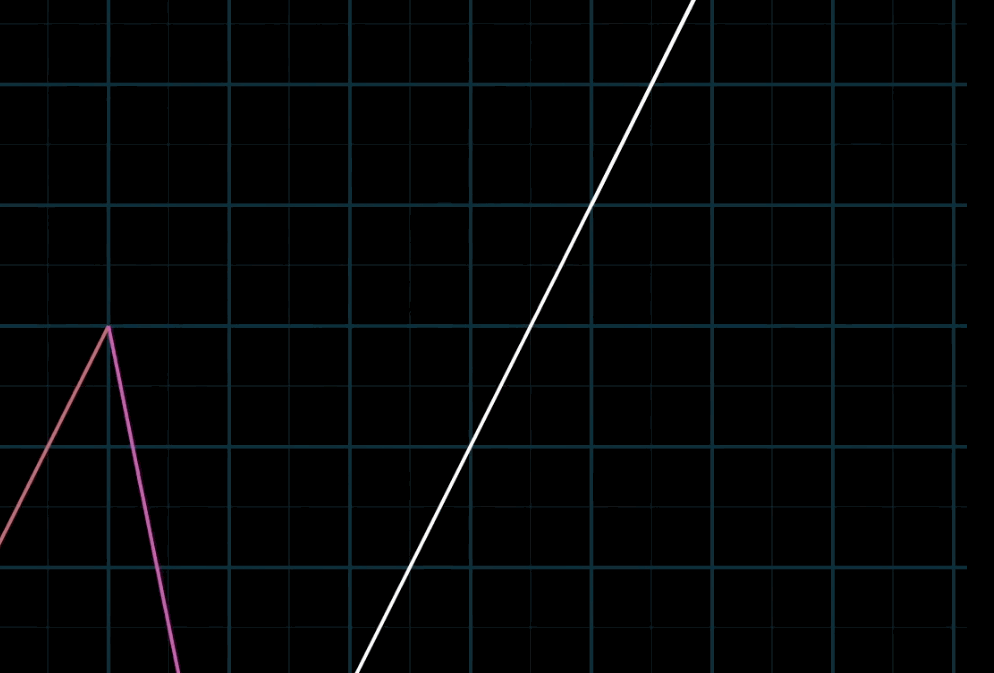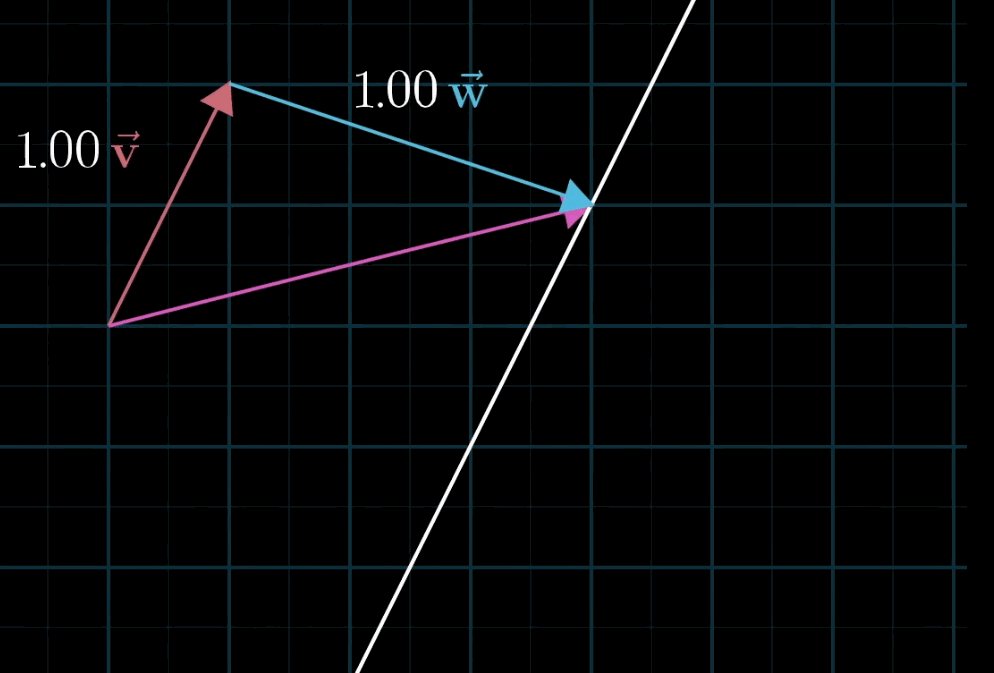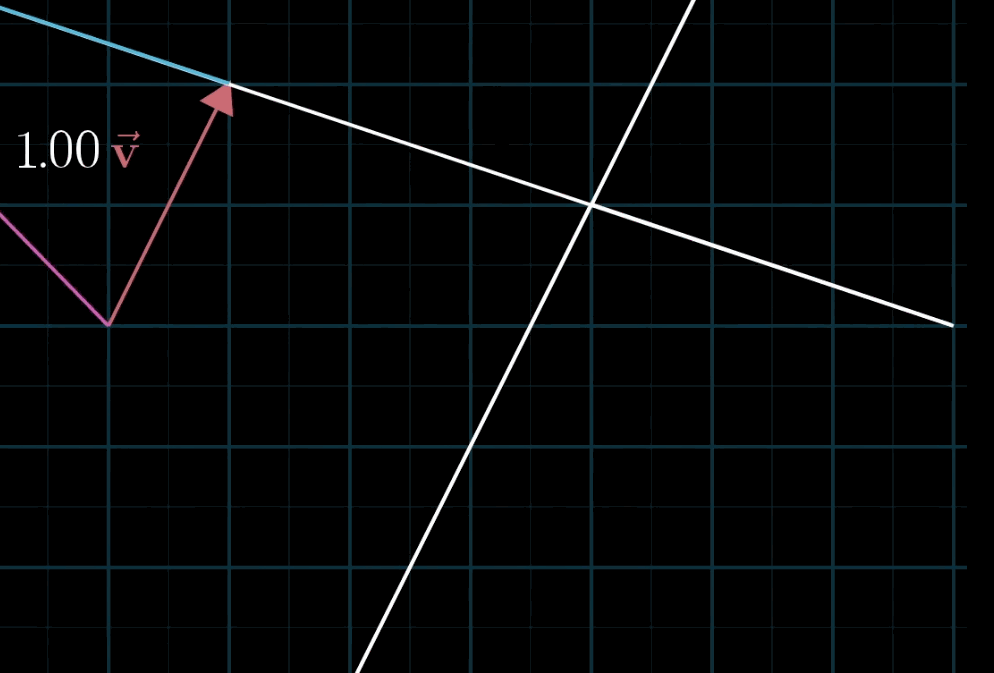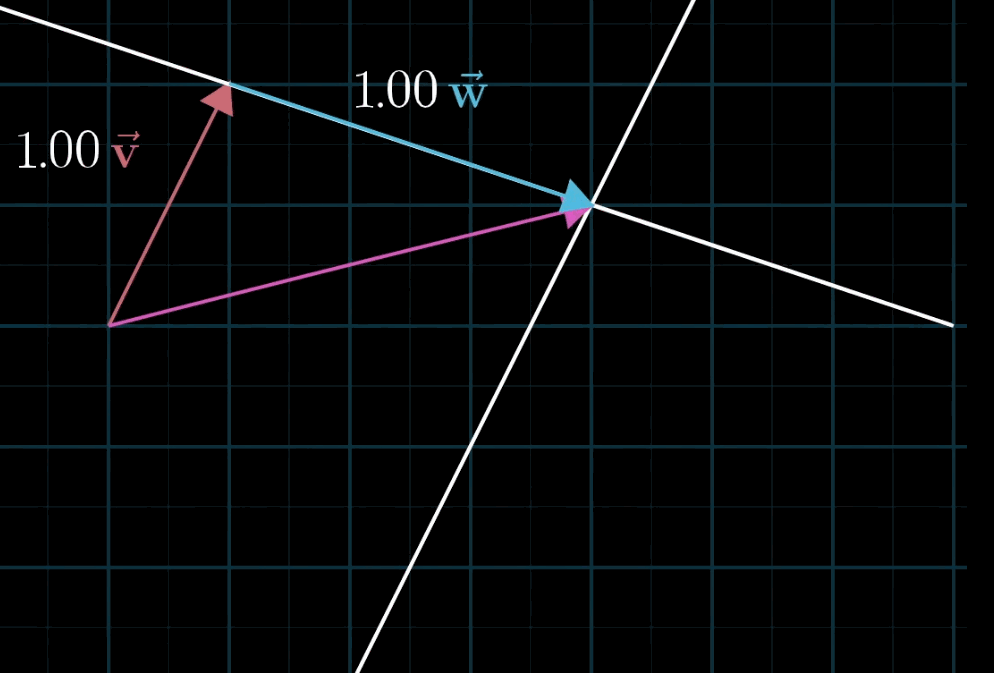
至于为什么被称为“线性”,有一种几何直观:如果你固定其中一个标量,让另一个标量自由变化,所产生的向量终点会描出一条直线。(这里其实很不严谨,具体定义请参阅课本。)
空间的基 (Basis)
对于我们常见的笛卡尔坐标系,有一组最直观的基:${ \hat{\imath},{\hat{\jmath}} }$,即单位向量 $\hat{\imath}=(1,0)$ 和 $\hat{\jmath}=(0,1)$,通过$\hat{\imath}$和${\hat{\jmath}}$的拉伸与相加可以组成笛卡尔坐标系中的任意一个向量。(上述的任意两个不共线的非零向量也可以作为二维空间的一组基。)
张成的空间 (Span)
同理,我们可以选择不同的基向量,而这些基向量构成的空间就称为其张成的空间。张成二字比较拗口,可以类比为延伸或扩展。直观来看,就是本文所有图中的网格。笛卡尔坐标系就是一个由单位坐标${ \hat{\imath},{\hat{\jmath}} }$张成的空间(同时也是上述任意两个不共线的非零向量所张成的空间)。所有可以表示为给定向量(基)线性组合(刚刚讲了这个概念)的向量的集合,被称为给定向量(基)张成的空间。
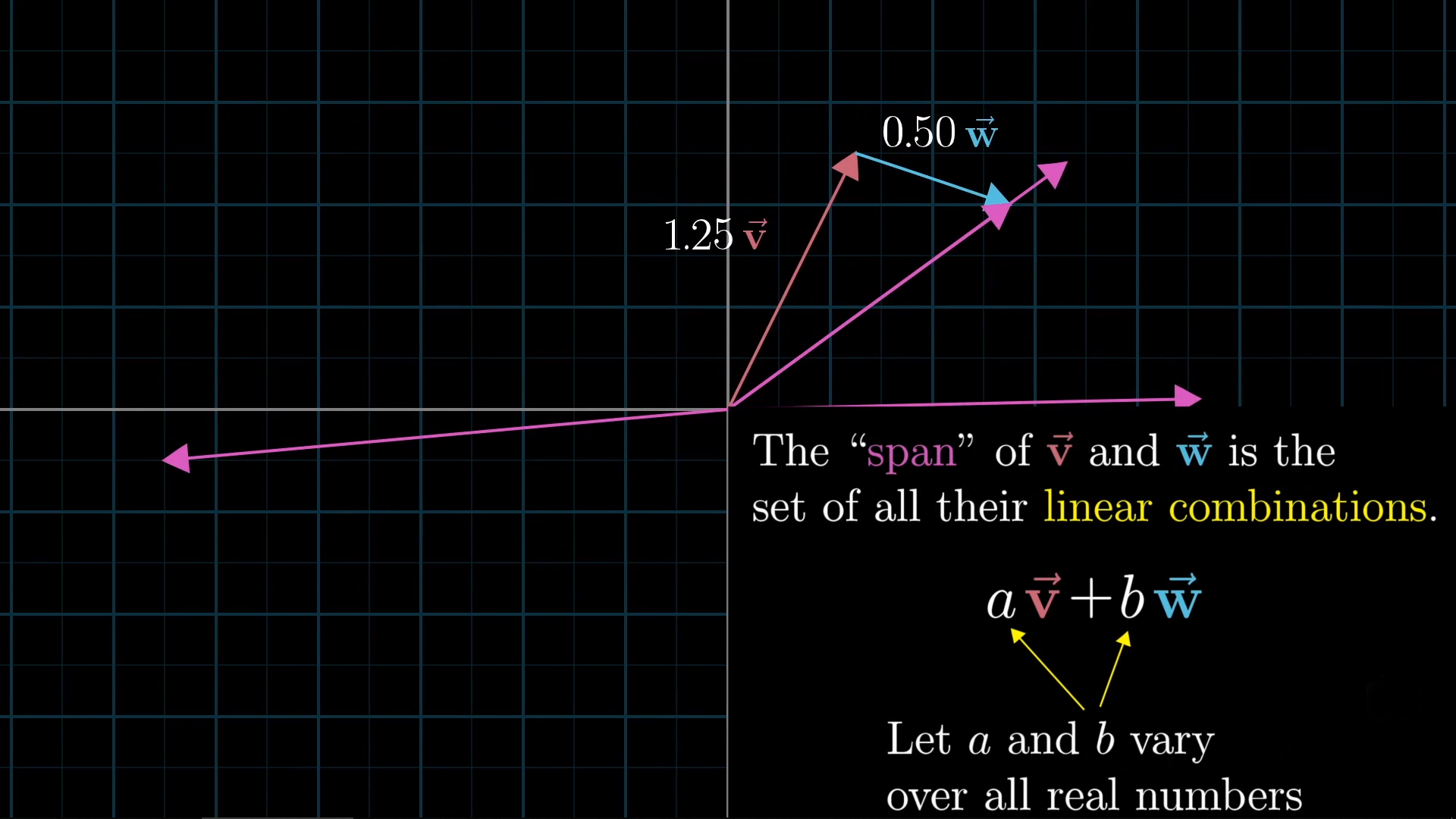
如果你继续思考一下,会发现一个特点:**并不是每一组给定向量都可以张成一个空间**,若这两个向量共线(2D),共面(3D),它们就只能被限制在一个直线或面中,类似于“降维打击”(这也是我强调不共线且向量非零的原因)。通过这个直观的思考可以引出以下概念:
线性相关
关于什么是线性相关,有两种表达:
- 你有多个向量,并且可以移除其中一个而不减小张成的空间(即2D共线或3D共面),我们称它们(这些向量)线性相关。
- 其中一个向量,可以表示为其他向量的线性组合,因为这个向量已经落在其他向量张成的空间之中。
从统计学角度来说,就是指这些向量之中有冗余。即在这一堆向量中,我们只需要其中几个(取决于维度)就可以表示所有其他的向量。
由此,我们可以得出以下部分:
向量空间中一组基的严格定义
向量空间的一组基是张成该空间的一个线性无关向量集。
在线性代数中,基(basis)(也称为基底)是描述、刻画向量空间的基本工具。向量空间的基是它的一个特殊的子集,基的元素称为基向量。向量空间中任意一个元素,都可以唯一地表示成基向量的线性组合。如果基中元素个数有限,就称向量空间为有限维向量空间,将元素的个数称作向量空间的维数。 使用基底可以便利地描述向量空间。
用这样的步骤来慢慢导出这个定义,个人感觉,远比在课堂的第一分钟就将这句让你迷惑的话丢给你好的多,抽象的东西只有在慢慢推倒中你才能发现它的精巧之处,非常优雅且迷人。
矩阵与线性变换
Unfortunately, no one can be told what the Matrix is. You have to see it for yourself.
很遗憾,矩阵是什么是说不清的。你必须得自己亲眼看看。
矩阵,最直观的理解当然是一个写成方阵的数字 $\begin{pmatrix}1&0 \\ 0&1 \end{pmatrix}$,这几节的核心是为了说明:矩阵其实就是一种向量变换(至于什么是变换下面会讲),并附带一种不用死记硬背的考虑矩阵向量乘法的方法。
变换
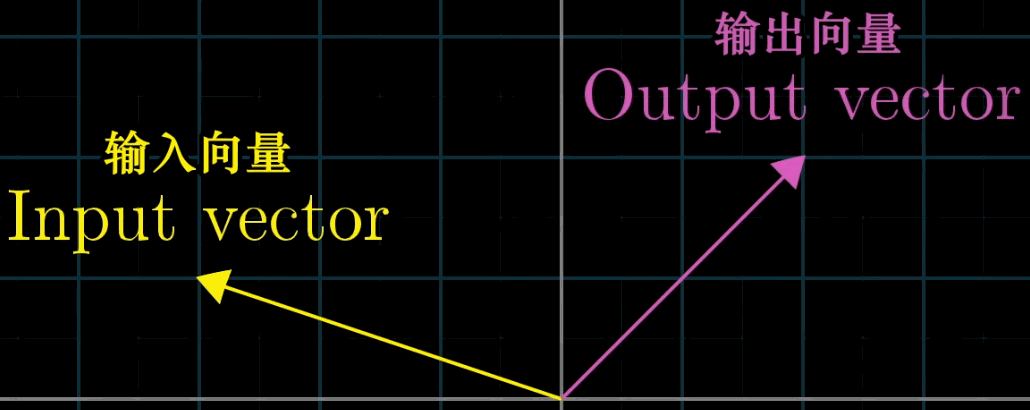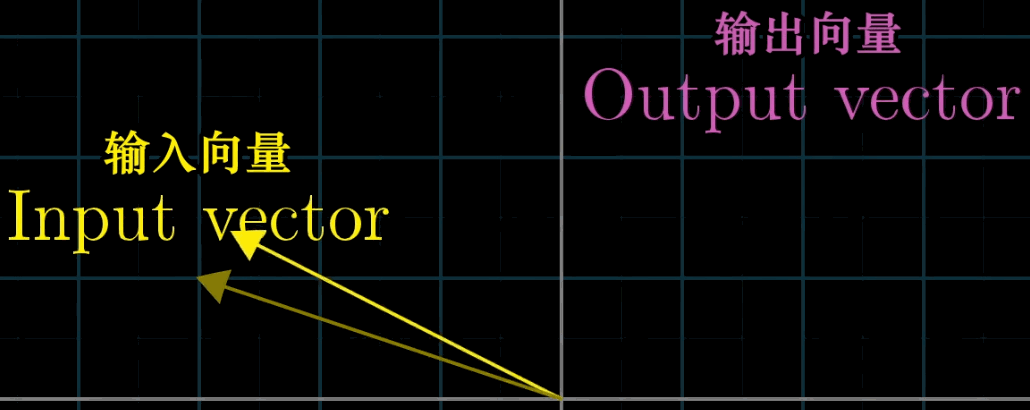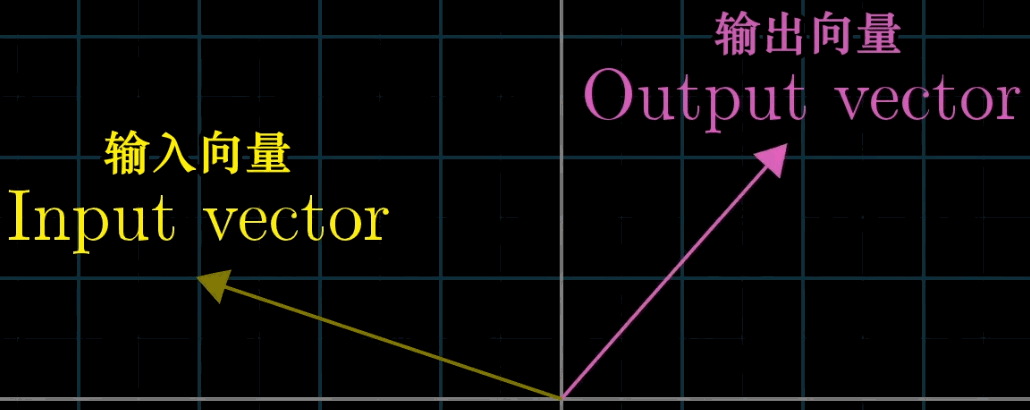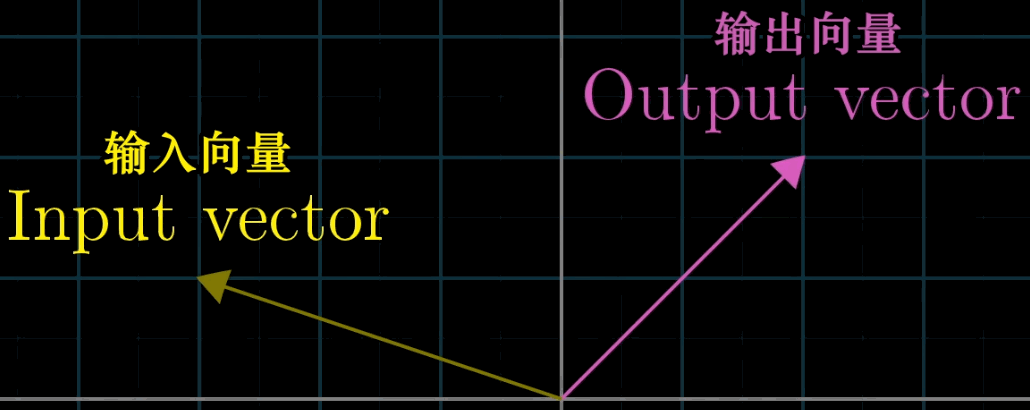
变换本质上是函数(下左图)的一种花哨的说法,它接受输入内容,并输出对应结果,特别的,在矩阵变换(下右图)中,我们接受一个向量并且输出另一个向量。

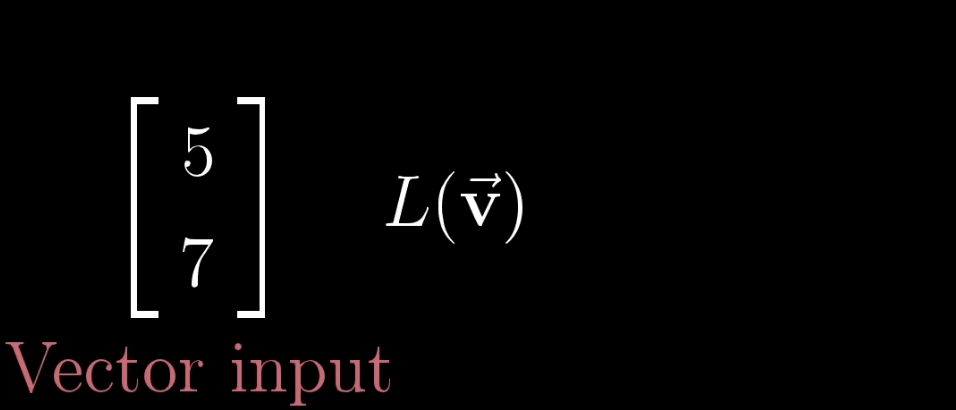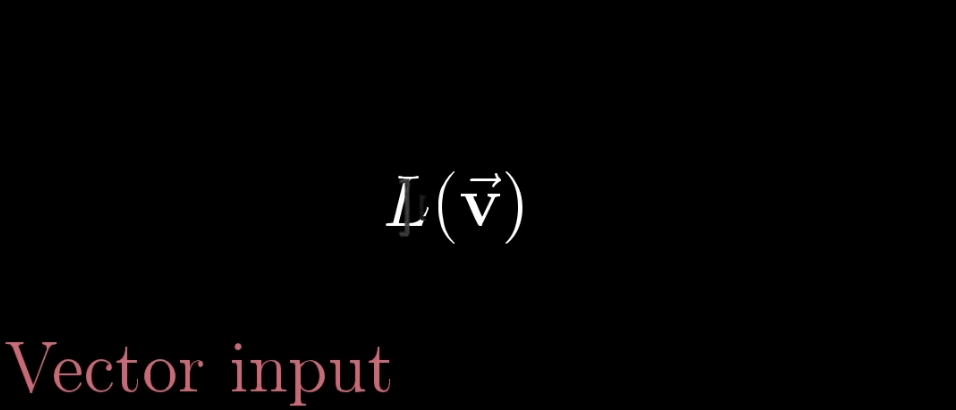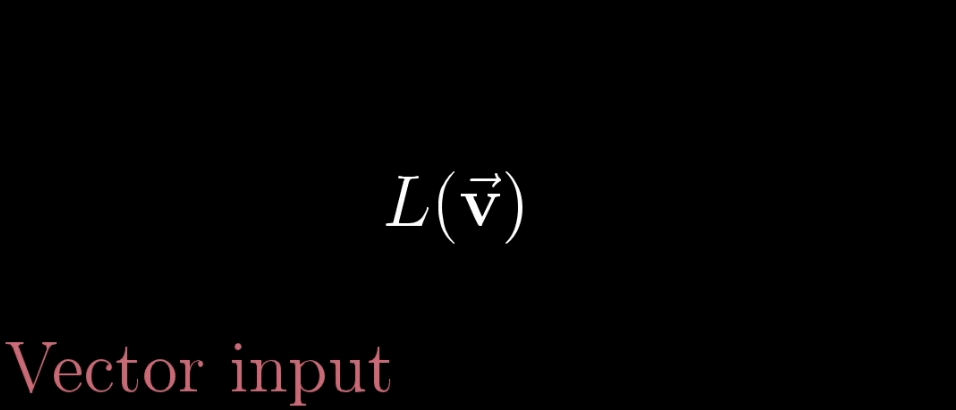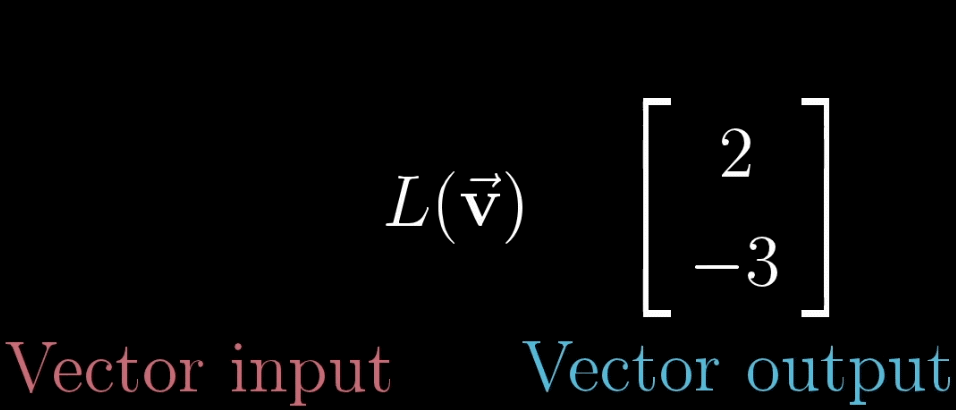
那既然变换和函数意义相同,为什么要用多余的术语困惑我们呢?因为使用变换是在暗示以特定方式来可视化这一输入$\to$输出关系。一种理解“向量的函数”的方法就是就是使用运动。
这世界上有非常多优美的变换,如果你将他们可视化,就能得到下图:

线性变换
我们说具有以下两个性质的就是线性变换(直观可视化如下图):
- 直线在变换后仍然保持为直线,不能有所弯曲。
- 原点必须保持固定

用一句话总结就是:线性变换是保持网格线平行且等距分布的变换(如果变换后保持直线不变但原点改变则为仿射变换,即线性变换+平移)。
如何用数值描述线性变换
这里需要使用上一节提到的工具,空间的基,也就是单位向量(基向量):$\hat{\imath}=(1,0)$ 和 $\hat{\jmath}=(0,1)$
对线性变换,我们只需要关注两个基向量 $\hat{\imath}$ 和 $\hat{\jmath}$变换后的位置即可。例如,$\hat{\imath}$ 变换到$(3,1)$的位置,$\hat{\jmath}$ 变换到$(1,2)$的位置,将$\hat{\imath}$变换后的坐标竖起来作为方阵的第一列(绿色表示),$\hat{\jmath}$变换后的坐标竖起来作为方阵的第二列(红色表示),得到矩阵$\begin{pmatrix}\color{green}3&\color{red}1 \\ \color{green}1&\color{red}2 \end{pmatrix}$。假设我们想要知道目标向量$(-1,2)$进行变换后的位置,那么这个矩阵就是对变换过程最好的描述,一图胜千言。
- Step1: 绿色$\hat{\imath}$(x轴)进行移动(变换)
- Step2: 红色$\hat{\jmath}$(y轴)进行移动(变换)
- Step3: 目标向量x轴坐标值与$\hat{\imath}$变换后向量进行向量乘法
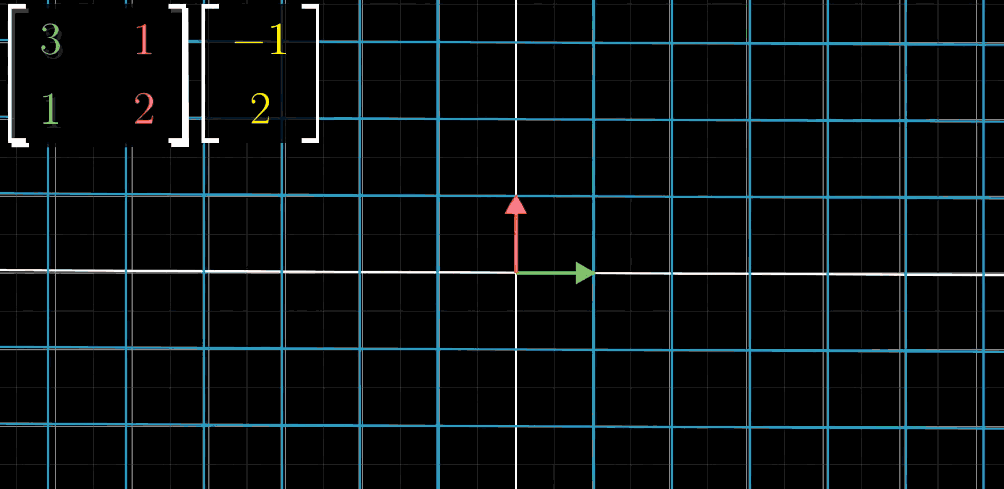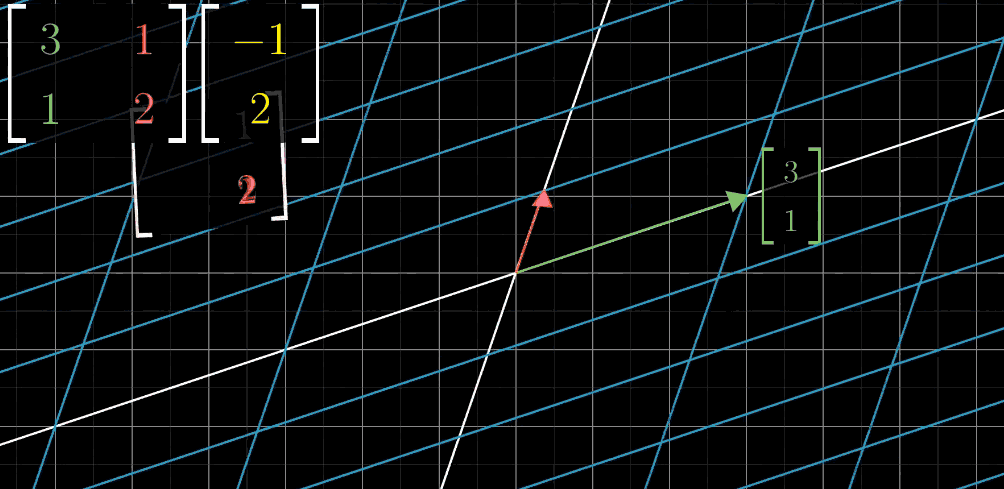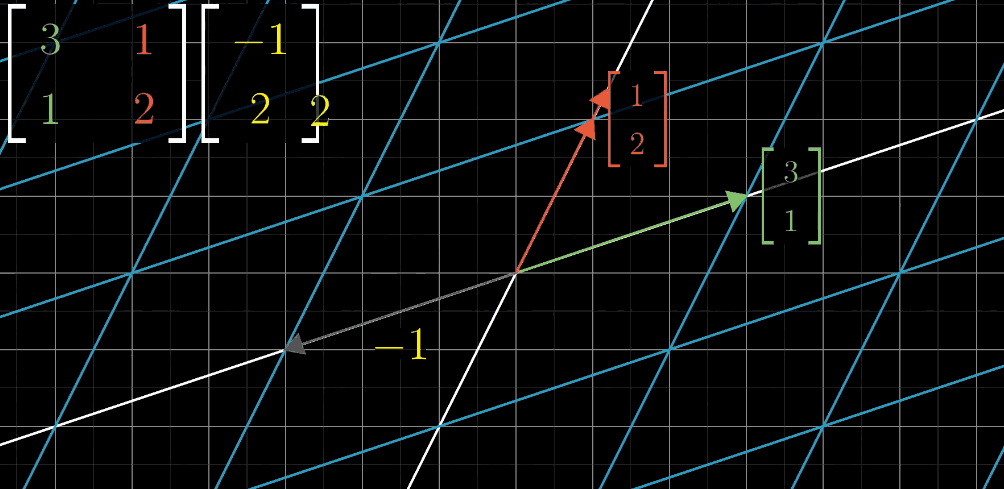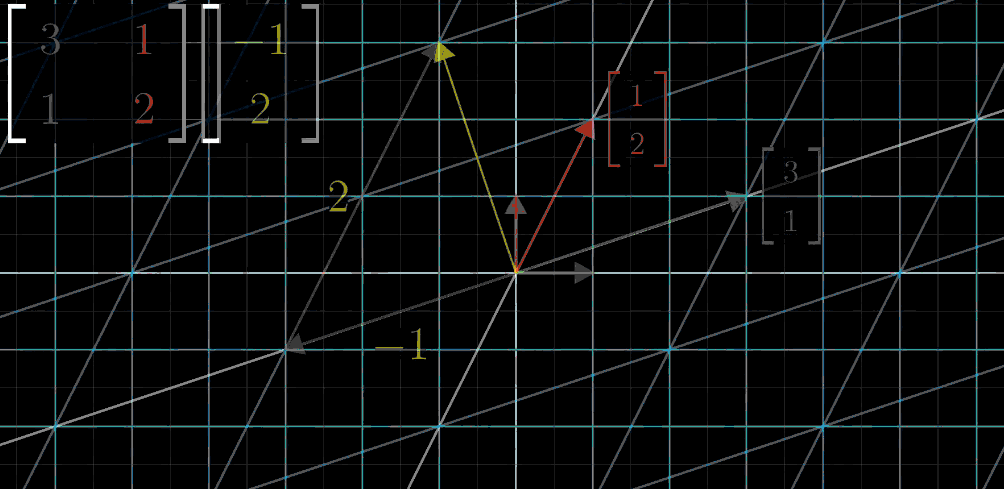
- Step4: 目标向量y轴坐标值与$\hat{\jmath}$变换后向量进行向量乘法
- Step5: 两者进行向量加法,得到线性变换结果
更加一般的情况,我们用变量来代替其中的具体值,其中绿色代表$\hat{\imath}$变换后的向量,红色代表$\hat{\jmath}$变换后的向量:
$\begin{pmatrix}\color{green}a&\color{red}b \\ \color{green}c&\color{red}d \end{pmatrix}\begin{pmatrix} x \\ y\end{pmatrix} = \underbrace{x \begin{pmatrix}\color{green}a \\ \color{green}c \end{pmatrix} + y \begin{pmatrix} \color{red}b \\ \color{red}d \end{pmatrix}}_{\text{直观的部分这里}} = \begin{pmatrix}\color{green}{a}\color{black}{x}+\color{red}{b}\color{black}{y} \\ \color{green}{c}\color{black}{x}+\color{red}{d}\color{black}{y}\end{pmatrix}$
上面的公式就是我们常说的矩阵乘法公式,现在,不要强行背诵,结合可视化的直观动图,你一辈子都不会忘记的。
线性的严格定义
在给出一个数学化抽象的解释前,先做一下总结:
- 线性变换是操纵空间的一种手段,它保持网格线平行且等距分布,并保持原点不动
- 矩阵是描述这种变换的一组数字,或者说一种描述线性变换的语言
在数学上,线性的严格定义如下述公式,这些性质,会在之后进行讨论,也可以在这里就进行一些思考,为什么说向量加法和向量乘法贯穿线性代数始终?
$L(\mathbf {\vec v} + \mathbf{\vec w}) = L(\mathbf {\vec v}) + L(\mathbf {\vec w}) \qquad 可加性(对加法封闭)$
$L(c \mathbf {\vec v}) = c L(\mathbf {\vec v}) \qquad 成比例(对数乘封闭)$
矩阵乘法与线性变换复合
It is my experience that proofs involving matrices can be shortened by 50% if one throws the matrices out.
据我的经验,如果丢掉矩阵的话,那些涉及矩阵的证明可以缩短一半。
复合变换
如果对一个向量先进行一次旋转变换,再进行一次剪切变换( $\hat {\imath}$保持$(1,0)$不变, $\hat{\jmath}$移动到坐标$(1,1)$),如下图所示:

那么如果通过旋转矩阵和剪切矩阵来求得这个符合矩阵呢?为了解决这个问题,我们定义这个过程叫做**矩阵的乘法**。
矩阵乘法的计算
在这里我们发现,矩阵乘法的变换顺序是从右往左读的(这一个常识很重要,你得明白这一点,有基本概念),也和我们熟知的复合函数形式 $f(g(x))$ 是一致的。
那么如何求解矩阵乘法呢?对线性代数有印象的同学现在能马上记起来那个稍显复杂的公式吗?如果有些忘记了,那么,现在,就有一个一辈子也忘不了的直观解释方法:
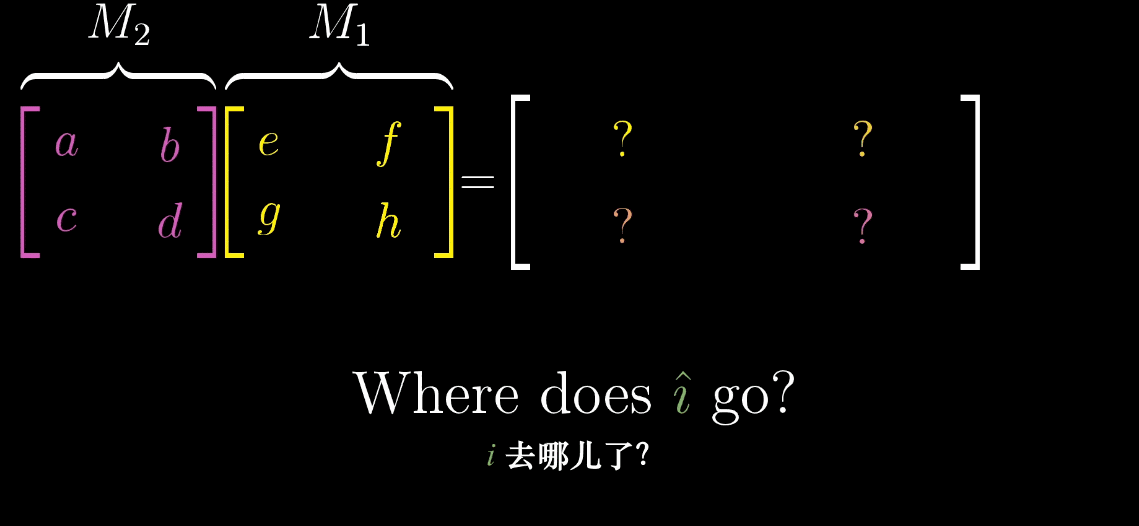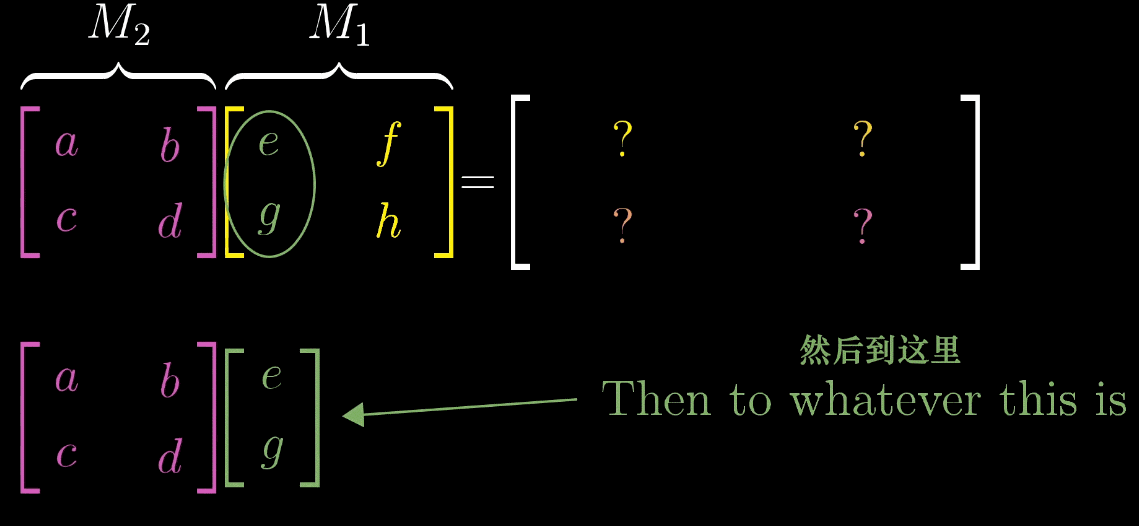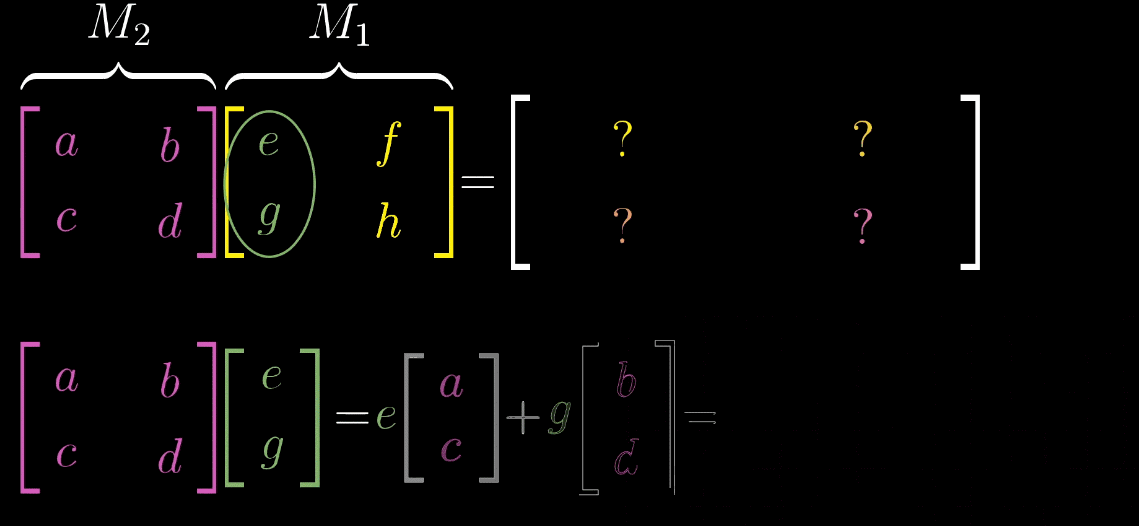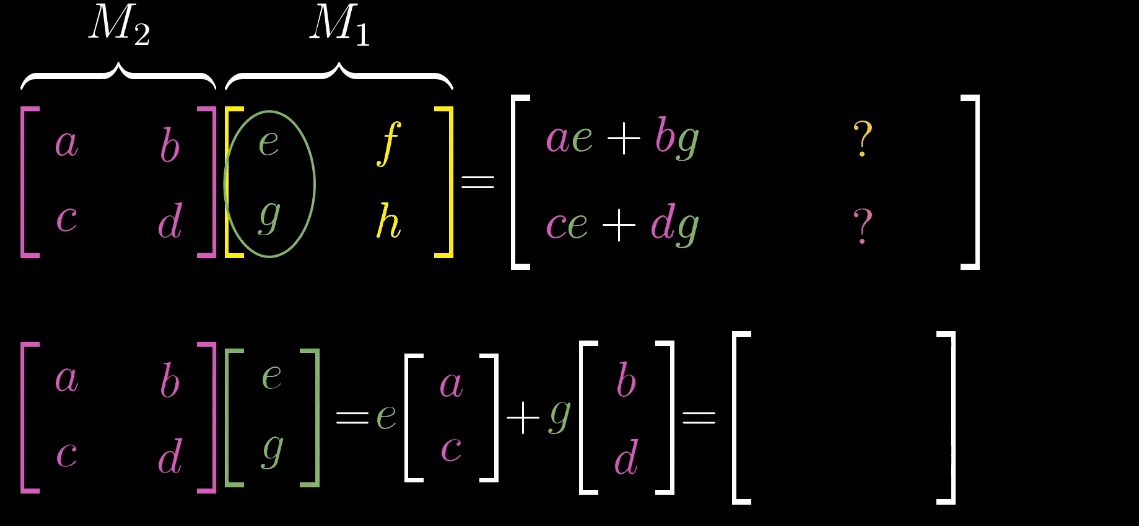
如图,$M_1$矩阵的第一列表示的是$\hat{\imath}$变换的位置,先把它拿出来,$M_2$矩阵看成对这个变换过的$\hat{\imath}$进行一次变换(按照前文的规则)。同理,针对$\hat{\jmath}$做一样的操作,就可以得出这个表达式。
矩阵乘法的运算规律
通常学生在学习矩阵乘法时都会记住上述公式并通过一些特定的运算加强记忆(包括我),但是在记忆这个过程前,我希望你能养成思考矩阵乘法意义的习惯,也就是两个变换相继作用。这能形成一个更好的概念性框架,并让你更容易理解矩阵乘积的性质。
举个栗子,矩阵相乘时,它们的先后顺序影响结果吗?有了上面的想法,可以自己试着在不进行计算的条件下思考一下,然后再尝试证明结合律与分配律是否成立。你会发现,原来线性代数是这么的直观,完全不需要计算。
未完待续……
