密码学初探-基于RUST的密码系统与算法简析
Introduction
密码学(Cryptography)一般可分为古典密码学和现代密码学。
其中,古典密码学,作为一种实用性艺术存在,其编码和破译通常依赖于设计者和敌手的创造力与技巧,并没有对密码学原件进行清晰的定义。古典密码学主要包含以下几个方面:
- 单表替换加密(Monoalphabetic Cipher)
- 多表替换加密(Polyalphabetic Cipher)
- 奇奇怪怪的加密方式
而现代密码学则起源于 20 世纪中后期出现的大量相关理论,1949 年香农(C. E. Shannon)发表了题为《保密系统的通信理论》的经典论文标志着现代密码学的开始。现代密码学主要包含以下几个方面:
- 对称加密(Symmetric Cryptography),以 DES,AES,RC4 为代表。
- 非对称加密(Asymmetric Cryptography),以 RSA,ElGamal,椭圆曲线加密为代表。
- 哈希函数(Hash Function),以 MD5,SHA-1,SHA-512 等为代表。
- 数字签名(Digital Signature),以 RSA 签名,ElGamal 签名,DSA 签名为代表。
其中,对称加密体制主要分为两种方式:
- 分组密码(Block Cipher),又称为块密码。
- 序列密码(Stream Cipher),又称为流密码。
一般来说,密码设计者的根本目标是保障信息及信息系统的
- 机密性(Confidentiality)
- 完整性(Integrity)
- 可用性(Availability)
- 认证性(Authentication)
- 不可否认性(Non-repudiation)
其中,前三者被称为信息安全的 CIA 三要素 。
本文主要介绍了仿射密码,流密码(RC4,LFSR+JK),分组密码(DES,AES),非对称加密(rsa)和密码协议(Diffie_Hellman)。 项目详细代码已于Github开源[1]。
仿射密码
原理
仿射密码的加密函数是 \(E(x)=(ax+b)\pmod m\),其中
- \(x\) 表示明文按照某种编码得到的数字
- \(a\) 和 \(m\) 互质
- \(m\) 是编码系统中字母的数目。
解密函数是 \(D(x)=a^{-1}(x-b)\pmod m\),其中 \(a^{-1}\) 是 \(a\) 在 \(\mathbb{Z}_{m}\) 群的乘法逆元。
下面我们以 \(E(x) = (5x + 8) \bmod 26\) 函数为例子进行介绍,加密字符串为 AFFINE CIPHER,这里我们直接采用字母表26个字母作为编码系统
| 明文 | A | F | F | I | N | E | C | I | P | H | E | R |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| x | 0 | 5 | 5 | 8 | 13 | 4 | 2 | 8 | 15 | 7 | 4 | 17 |
| \(y=5x+8\) | 8 | 33 | 33 | 48 | 73 | 28 | 18 | 48 | 83 | 43 | 28 | 93 |
| \(y\mod26\) | 8 | 7 | 7 | 22 | 21 | 2 | 18 | 22 | 5 | 17 | 2 | 15 |
| 密文 | I | H | H | W | V | C | S | W | F | R | C | P |
其对应的加密结果是 IHHWVCSWFRCP。
对于解密过程,正常解密者具有a与b,可以计算得到 \(a^{-1}\) 为 21,所以其解密函数是\(D(x)=21(x-8)\pmod {26}\) ,解密如下
| 密文 | I | H | H | W | V | C | S | W | F | R | C | P |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| \(y\) | 8 | 7 | 7 | 22 | 21 | 2 | 18 | 22 | 5 | 17 | 2 | 15 |
| \(x=21(y-8)\) | 0 | -21 | -21 | 294 | 273 | -126 | 210 | 294 | -63 | 189 | -126 | 147 |
| \(x\mod26\) | 0 | 5 | 5 | 8 | 13 | 4 | 2 | 8 | 15 | 7 | 4 | 17 |
| 明文 | A | F | F | I | N | E | C | I | P | H | E | R |
可以看出其特点在于只有 26 个英文字母。

Rust实现
1 | |
破解
首先,我们可以看到的是,仿射密码对于任意两个不同的字母,其最后得到的密文必然不一样,所以其也具有最通用的特点。当密文长度足够长时,我们可以使用频率分析的方法来解决。
其次,我们可以考虑如何攻击该密码。可以看出当\(a=1\) 时,仿射加密是凯撒加密。而一般来说,我们利用仿射密码时,其字符集都用的是字母表,一般只有26个字母,而不大于26的与26互素的个数一共有
\[ \phi(26)=\phi(2) \times \phi(13) = 12 \]
算上b的偏移可能,一共有可能的密钥空间大小也就是
\[ 12 \times 26 = 312 \]
一般来说,对于该种密码,我们至少得是在已知部分明文的情况下才可以攻击。下面进行简单的分析。
这种密码由两种参数来控制,如果我们知道其中任意一个参数,那我们便可以很容易地快速枚举另外一个参数得到答案。
但是,假设我们已经知道采用的字母集,这里假设为26个字母,我们还有另外一种解密方式,我们只需要知道两个加密后的字母 \(y_1,y_2\) 即可进行解密。那么我们还可以知道
\[ \begin{align} y_1 &= (ax_1+b)\pmod{26} \\ y_2 &= (ax_2+b)\pmod{26} \end{align} \]
两式相减,可得
\[ \begin{align} y_1-y_2 &= a(x_1-x_2)\pmod{26} \end{align} \]
这里 \(y_1,y_2\) 已知,如果我们知道密文对应的两个不一样的字符 \(x_1\) 与 \(x_2\) ,那么我们就可以很容易得到 \(a\) ,进而就可以得到 \(b\) 了。
流密码
流密码一般逐字节或者逐比特处理信息。一般来说
- 流密码的密钥长度会与明文的长度相同。
- 流密码的密钥派生自一个较短的密钥,派生算法通常为一个伪随机数生成算法。
需要注意的是,流加密目前来说都是对称加密。
伪随机数生成算法生成的序列的随机性越强,明文中的统计特征被覆盖的更好。
流密码加解密非常简单,在已知明文的情况下,可以非常容易地获取密钥流。
流密码的关键在于设计好的伪随机数生成器。一般来说,伪随机数生成器的基本构造模块为反馈移位寄存器。当然,也有一些特殊设计的流密码,比如 RC4。
反馈移位寄存器
一般的,一个 n 级反馈移位寄存器如下图所示
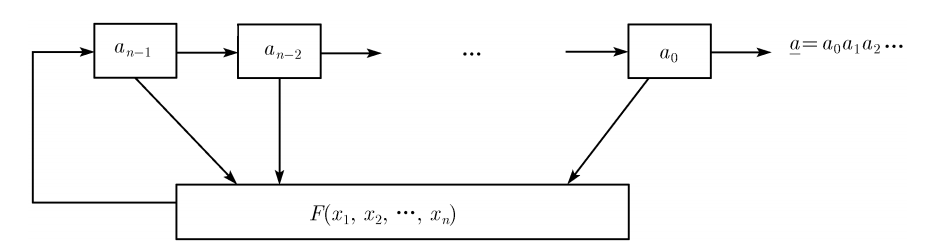
其中
- \(a_0\),\(a_1\),…,\(a_{n-1}\) 为初态。
- F 为反馈函数或者反馈逻辑。如果 F 为线性函数,那么我们称其为线性反馈移位寄存器(LFSR),否则我们称其为非线性反馈移位寄存器(NFSR)。
- \(a_{i+n}=F(a_i,a_{i+1},...,a_{i+n-1})\) 。
一般来说,反馈移位寄存器都会定义在某个有限域上,从而避免数字太大和太小的问题。因此,我们可以将其视为同一个空间中的变换,即
\((a_i,a_{i+1},...,a_{i+n-1}) \rightarrow (a_{i+1},...,a_{i+n-1},a_{i+n})\) . 对于一个序列来说,我们一般定义其生成函数为其序列对应的幂级数的和。
线性反馈移位寄存器 - LFSR
介绍
线性反馈移位寄存器的反馈函数一般如下
\[a_{i+n}=\sum\limits_{j=1}^{n}c_ja_{i+n-j}\]
其中,\(c_j\) 均在某个有限域 \(F_q\) 中。
既然线性空间是一个线性变换,我们可以得知这个线性变换为
\[ \begin{align} &\left[ a_{i+1},a_{i+2},a_{i+3}, \ldots,a_{i+n} \right] \\ &= \left[ a_{i},a_{i+1},a_{i+2}, \ldots,a_{i+n-1} \right]\left[ \begin{matrix} 0 & 0 & \cdots & 0 & c_n \\ 1 & 0 & \cdots & 0 & c_{n-1} \\ 0 & 1 & \cdots & 0 & c_{n-2} \\ \vdots & \vdots & \ddots & \vdots & \vdots \\ 0 & 0 & \cdots & 1 & c_1 \end{matrix} \right] \\ &= \left[ a_{0},a_{1},a_{2}, \ldots,a_{n-1} \right]\left[ \begin{matrix} 0 & 0 & \cdots & 0 & c_n \\ 1 & 0 & \cdots & 0 & c_{n-1} \\ 0 & 1 & \cdots & 0 & c_{n-2} \\ \vdots & \vdots & \ddots & \vdots & \vdots \\ 0 & 0 & \cdots & 1 & c_1 \end{matrix} \right]^{i+1} \end{align} \]
进而,我们可以求得其特征多项式为
\[f(x)=x^n-\sum\limits_{i=1}^{n}c_ix^{n-i}\]
同时,我们定义其互反多项式为
\[\overline f(x)=x^nf(\frac{1}{x})=1-\sum\limits_{i=1}^{n}c_ix^{i}\]
我们也称互反多项式为线性反馈移位寄存器的联结多项式。
这里有一些定理需要我们记一下,感兴趣的可以自行推导。
样例
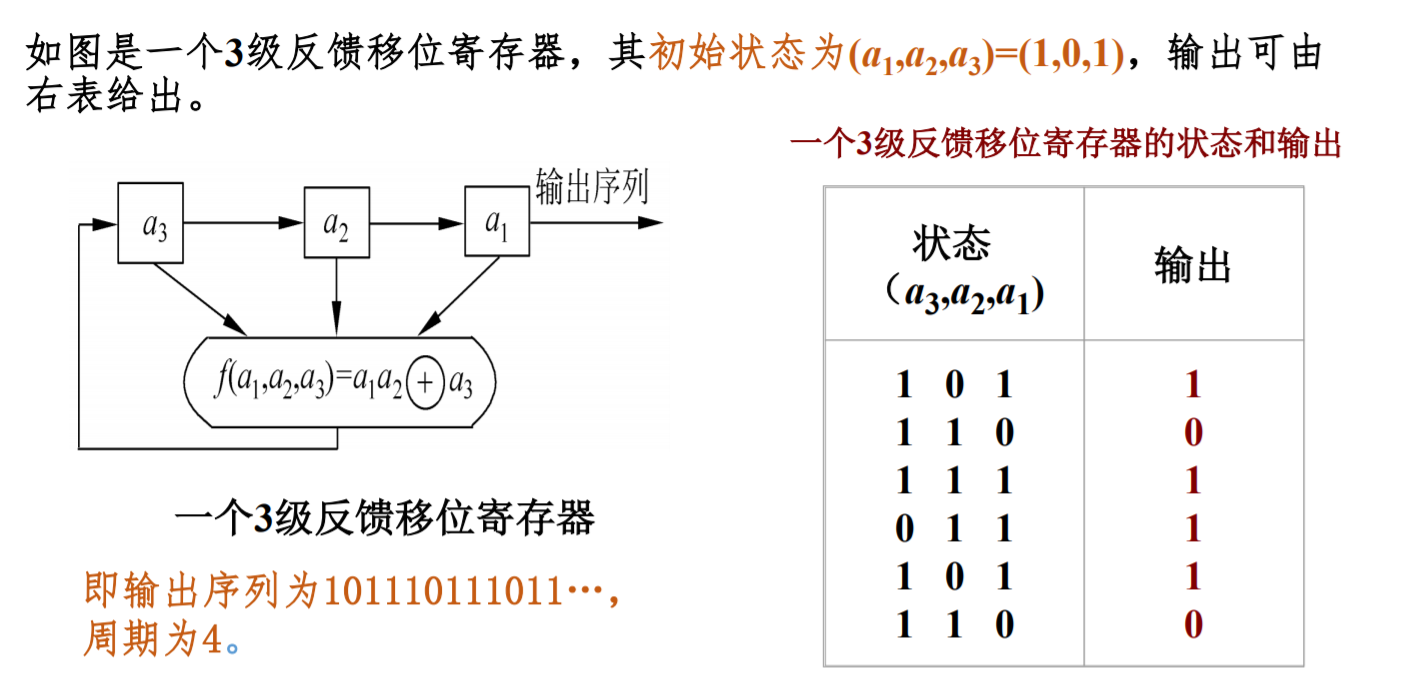
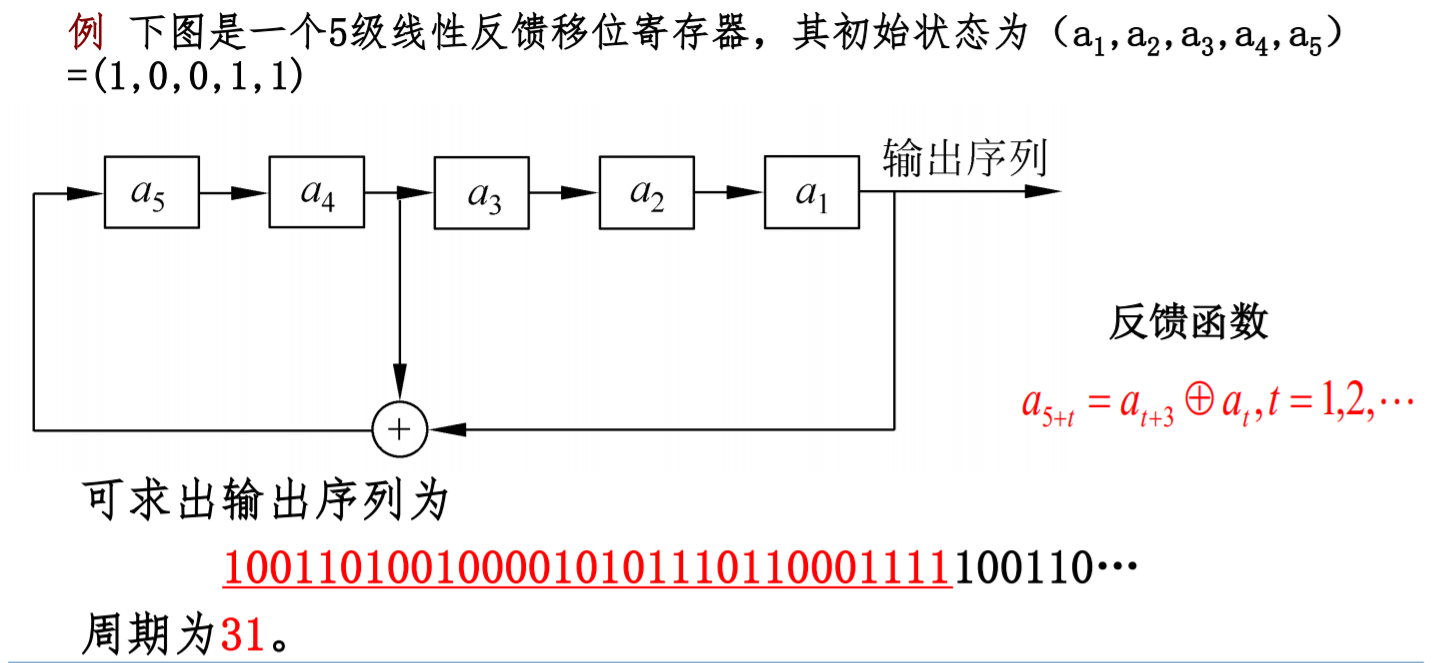
特征多项式与生成函数
已知某个 n 级线性反馈移位寄存器的特征多项式,那么该序列对应的生成函数为
\[A(x)=\frac{p(x)}{\overline f(x)}\]
其中,\(p(x)=\sum\limits_{i=1}^{n}(c_{n-i}x^{n-i}\sum\limits_{j=1}^{i}a_jx^{j-1})\)。可以看出 p(x) 完全由初始状态和反馈函数的系数决定。
序列周期与生成函数
序列的的周期为其生成函数的既约真分式的分母的周期。
对于 n 级线性反馈移位寄存器,最长周期为 \(2^{n}-1\)(排除全零)。达到最长周期的序列一般称为 m 序列。
特殊性质
- 将两个序列累加得到新的序列的周期为这两个序列的周期的和。
- 序列是 n 级 m 序列,当且仅当序列的极小多项式是 n 次本原多项式。
B-M 算法
一般来说,我们可以从两种角度来考虑 LFSR
- 密钥生成角度,一般我们希望使用级数尽可能低的 LFSR 来生成周期大,随机性好的序列。
- 密码分析角度,给定一个长度为 n 的序列 a,如何构造一个级数尽可能小的 LFSR 来生成它。其实这就是 B-M 算法的来源。
一般来说,我们定义一个序列的线性复杂度如下
- 若 s 为一个全零序列,则线性复杂度为0。
- 若没有 LFSR 能生成 s,则线性复杂度为无穷。
- 否则,s 的线性复杂度为生成 L(s) 的最小级的 LFSR。
BM 算法的要求我们需要知道长度为 2n 的序列。其复杂度
- 时间复杂度:O(n^2) 次比特操作
- 空间复杂度:O(n) 比特。
关于 BM 算法的细节,后续添加,目前处于学习过程中。
但是其实如果我们知道了长度为 2n 的序列,我们也可以一种比较笨的方法来获取原先的序列。不妨假设已知的序列为\(a_1,...,a_{2n}\),我们可以令
\[S_1=(a_1,...,a_n)\]
\[S_2=(a_2,...,a_{n+1})\]
…
\[S_{n+1}=(a_{n+1},...,a_{2n})\]
那么我们可以构造矩阵 \(X=(S_1,...,S_n)\),那么
\[S_{n+1}=(c_n,...,c_1)X\]
所以
\[(c_n,...,c_1)=S_{n+1}X^{-1}\]
进而我们也就知道了 LFSR 的反馈表达式,进而我们就可以推出初始化种子。
非线性反馈移位寄存器
介绍
为了使得密钥流输出的序列尽可能复杂,会使用非线性反馈移位寄存器,常见的有三种
- 非线性组合生成器,对多个 LFSR 的输出使用一个非线性组合函数
- 非线性滤波生成器,对一个 LFSR 的内容使用一个非线性组合函数
- 钟控生成器,使用一个(或多个)LFSR 的输出来控制另一个(或多个)LFSR 的时钟
非线性组合生成器
简介
组合生成器一般如下图所示。
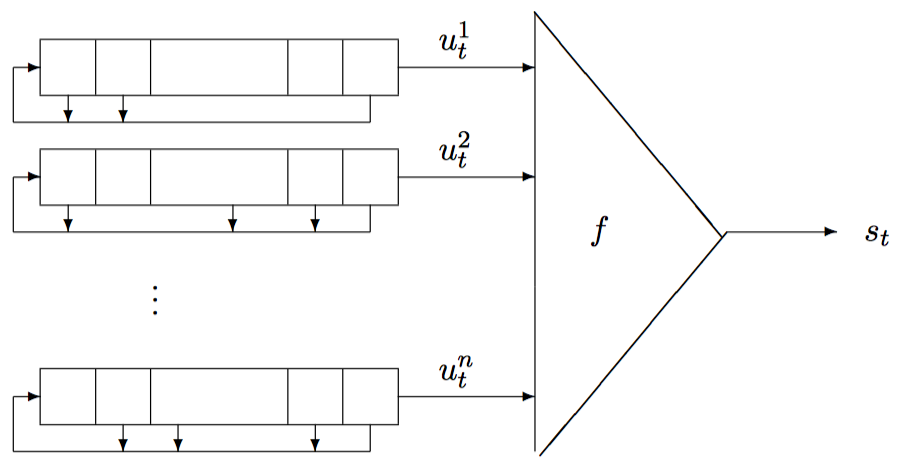
JK触发器
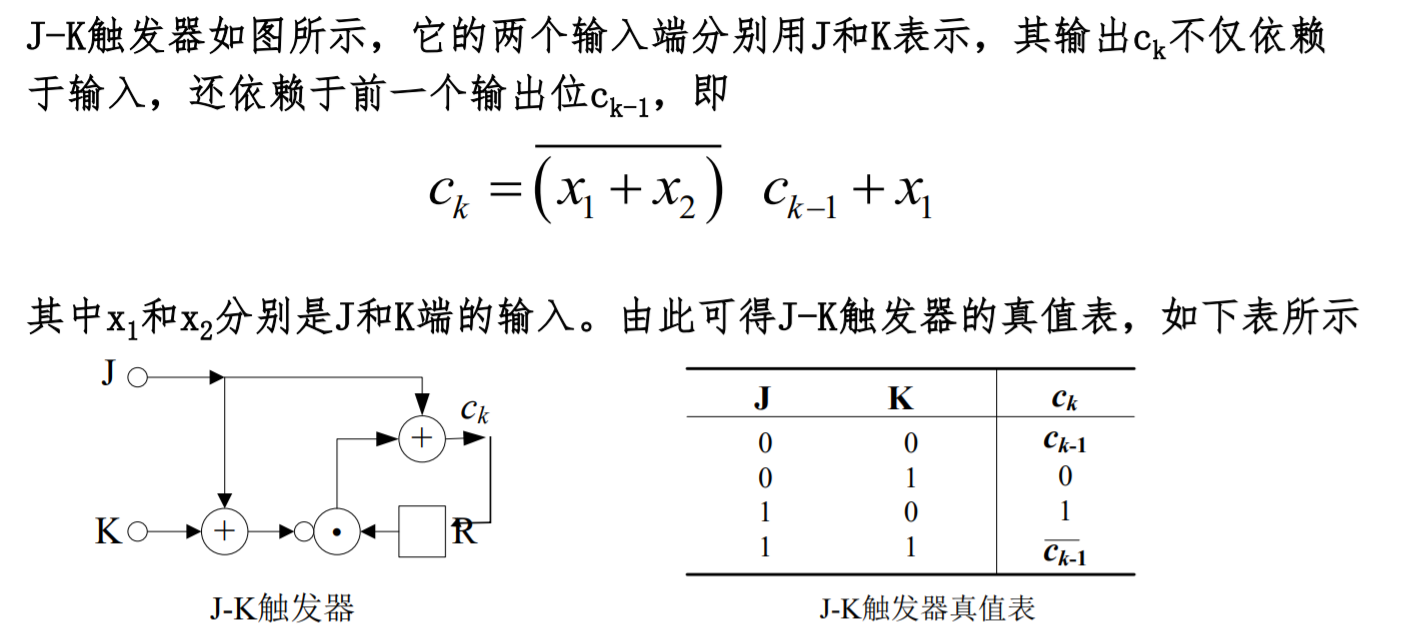
利用J-K触发器的非线性序列生成器
样例

Rust实现
1 | |
RC4
基本介绍
RSA 由 Ron Rivest 设计,加解密使用相同的密钥,因此也属于对称加密算法。它是面向字节的流密码,密钥长度可变,非常简单,但也很有效果。RC4 算法曾广泛应用于 SSL/TLS 协议和 WEP/WPA 协议,但由于RC4算法存在弱点,2015年2月所发布的 RFC 7465 规定禁止在TLS中使用RC4加密算法。
基本流程
RC4 主要包含三个流程
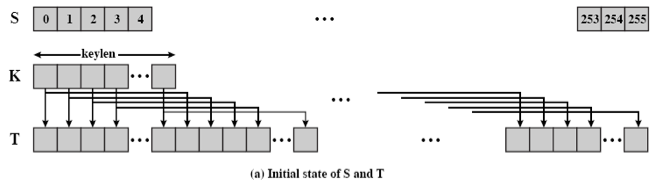
- 初始化 S 和 T 数组。
- 初始化置换 S。
- 生成密钥流。
初始化 S 和 T 数组
初始化 S 和 T 的代码如下
1 | |
初始化置换 S
1 | |
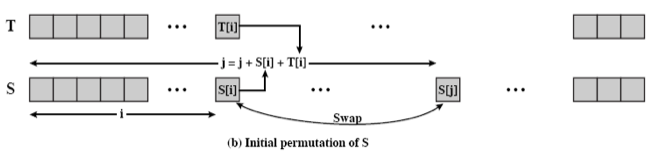
生成流密钥
1 | |

我们一般称前两部分为 KSA ,最后一部分是 PRGA。
Rust实现
1 | |
块加密
概述
所谓块加密就是每次加密一块明文,常见的加密算法有
- IDEA 加密
- DES 加密
- AES 加密
块加密也是对称加密。
其实,我们也可以把块加密理解一种特殊的替代密码,但是其每次替代的是一大块。而正是由于一大块,明文空间巨大,而且对于不同的密钥,我们无法做一个表进行对应相应的密文,因此必须得有 复杂 的加解密算法来加解密明密文。
而与此同时,明文往往可能很长也可能很短,因此在块加密时往往需要两个辅助
- padding,即 padding 到指定分组长度
- 分组加密模式,即明文分组加密的方式。
填充规则
正如我们之前所说,在分组加密中,明文的长度往往并不满足要求,需要进行 padding,而如何 padding 目前也已经有了不少的规定。
常见的 填充规则 如下。需要注意的是,即使消息的长度是块大小的整数倍,仍然需要填充。
一般来说,如果在解密之后发现 Padding 不正确,则往往会抛出异常。我们也因此可以知道 Paddig 是否正确。
Pad with bytes all of the same value as the number of padding bytes (PKCS5 padding)
1 | |
Pad with 0x80 followed by zero bytes (OneAndZeroes Padding)
1 | |
这里其实就是和 md5 和 sha1 的 padding 差不多。
Pad with zeroes except make the last byte equal to the number of padding bytes
1 | |
Pad with zero (null) characters
1 | |
Pad with spaces
1 | |
工作模式
分组密码的工作模式是:根据不同的数据格式和安全性要求, 以一个具体的分组密码算法为基础构造一个分组密码系统的方法。分组密码的工作模式应当力求简单, 有效和易于实现,需要采用适当的工作模式来隐蔽明文的统计特性、数据的格式等,降低删除、重放、插入和伪造成功的机会。
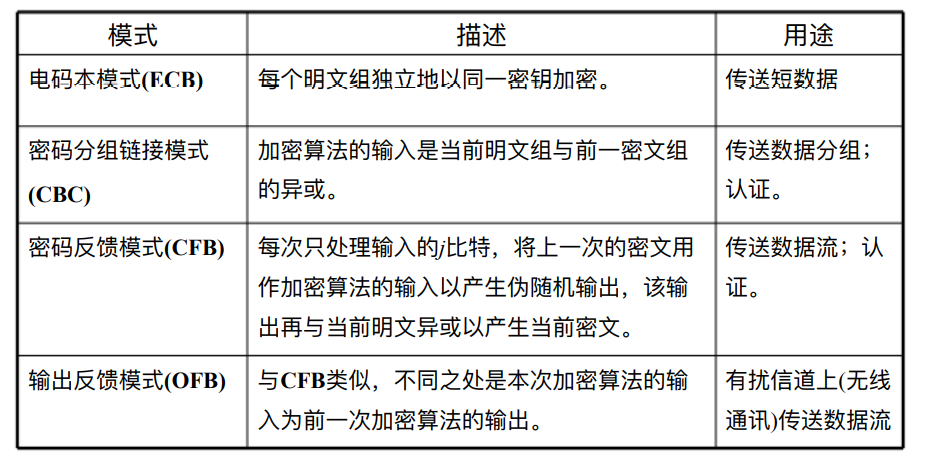
分组密码的主要工作模式:
- 电码本(ECB)模式
- 密码分组链接(CBC)模式
- 密码反馈(CFB)模式
- 输出反馈(OFB)模式
- 计数器(CTR)模式
基本策略
在分组密码设计时,充分使用了 Shannon 提出的两大策略:混淆与扩散两大策略。
混淆
混淆,Confusion,将密文与密钥之间的统计关系变得尽可能复杂,使得攻击者即使获取了密文的一些统计特性,也无法推测密钥。一般使用复杂的非线性变换可以得到很好的混淆效果,常见的方法如下
- S 盒
- 乘法
扩散
扩散,Diffusion,使得明文中的每一位影响密文中的许多位。常见的方法有
- 线性变换
- 置换
- 移位,循环移位
常见加解密结构
目前块加密中主要使用的是结构是
- 迭代结构,这是因为迭代结构便于设计与实现,同时方便安全性评估。
迭代结构
概述
迭代结构基本如下,一般包括三个部分
- 密钥置换
- 轮加密函数
- 轮解密函数
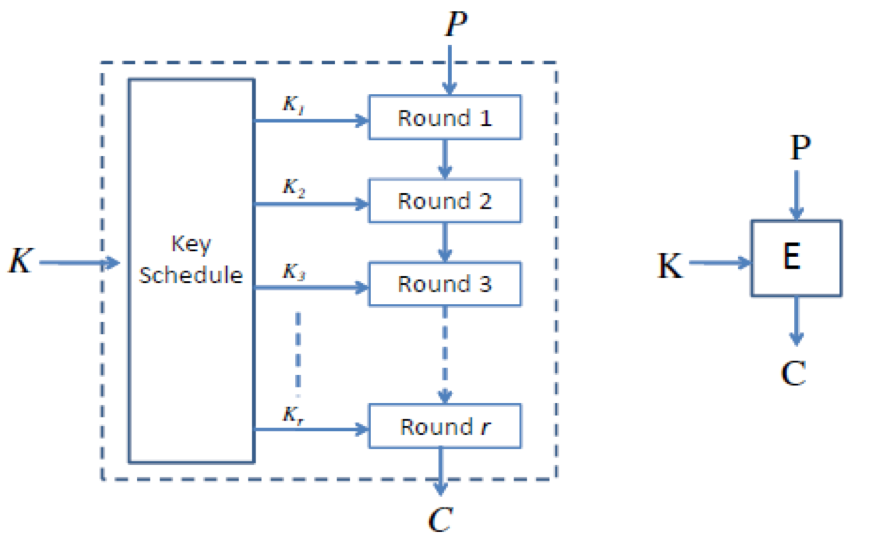
轮函数
目前来说,轮函数主要有主要有以下设计方法
- Feistel Network,由 Horst Feistel 发明,DES 设计者之一。
- DES
- Substitution-Permutation Network(SPN)
- AES
- 其他方案
密钥扩展
目前,密钥扩展的方法有很多,没有见到什么完美的密钥扩展方法,基本原则是使得密钥的每一个比特尽可能影响多轮的轮密钥。
DES
基本介绍
Data Encryption Standard(DES),数据加密标准,是典型的块加密,其基本信息如下
- 输入 64 位。
- 输出 64 位。
- 密钥 64 位,使用 64 位密钥中的 56 位,剩余的 8 位要么丢弃,要么作为奇偶校验位。
- Feistel 迭代结构
- 明文经过 16 轮迭代得到密文。
- 密文经过类似的 16 轮迭代得到明文。
基本流程
给出一张简单的 DES 流程图。
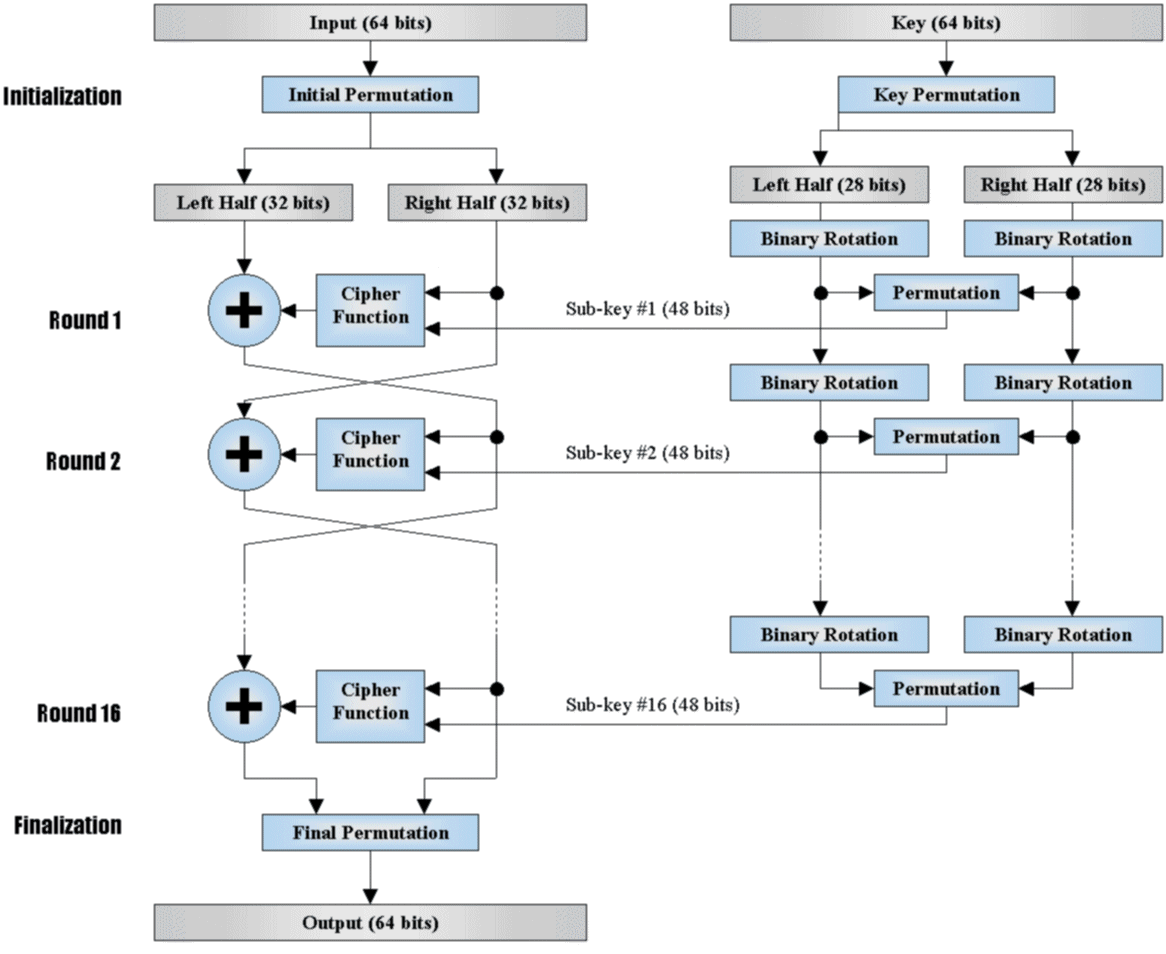
加密
我们可以考虑一下每一轮的加密过程
\[L_{i+1}=R_i\]
\[R_{i+1}=L_i\oplus F(R_i,K_i)\]
那么在最后的 Permutation 之前,对应的密文为\((R_{n+1},L_{n+1})\)。
解密
那么解密如何解密呢?首先我们可以把密文先进行逆置换,那么就可以得到最后一轮的输出。我们这时考虑每一轮
\[R_i=L_{i+1}\]
\[L_i=R_{i+1}\oplus F(L_{i+1},K_i)\]
因此,\((L_0,R_0)\) 就是加密时第一次置换后的明文。我们只需要再执行逆置换就可以获得明文了。
可以看出,DES 加解密使用同一套逻辑,只是密钥使用的顺序不一致。
核心部件
DES 中的核心部件主要包括(这里只给出加密过程的)
- 初始置换
- F 函数
- E 扩展函数
- S 盒,设计标准未给出。
- P 置换
- 最后置换
其中 F 函数如下
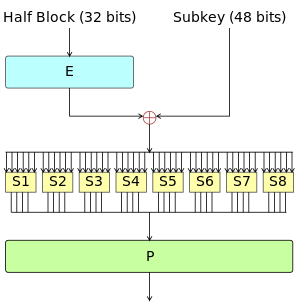
如果对 DES 更加感兴趣,可以进行更加仔细地研究。欢迎提供 PR。
衍生
在 DES 的基础上,衍生了以下两种加密方式
- 双重 DES
- 三种 DES
双重 DES
双重 DES 使用两个密钥,长度为 112 比特。加密方式如下
\[C=E_{k2}(E_{k1}(P))\]
但是双重 DES 不能抵抗中间相遇攻击,我们可以构造如下两个集合
\[I={E_{k1}(P)}\]
\[J=D_{k2}(C)\]
即分别枚举 K1 和 K2 分别对 P 进行加密和对 C 进行解密。
在我们对 P 进行加密完毕后,可以对加密结果进行排序,这样的复杂度为\(2^nlog(2^n)=O(n2^n)\)
当我们对 C 进行解密时,可以每解密一个,就去对应的表中查询。
总的复杂度为还是\(O(n2^n)\)。
三重 DES
三重 DES 的加解密方式如下
\[C=E_{k3}(D_{k2}(E_{k1}(P)))\]
\[P=D_{k1}(E_{k2}(D_{k3}(C)))\]
在选择密钥时,可以有两种方法
- 3 个不同的密钥,k1,k2,k3 互相独立,一共 168 比特。
- 2 个不同的密钥,k1 与 k2 独立,k3=k1,112 比特。
攻击方法
- 差分攻击
- 线性攻击
AES
基本介绍
Advanced Encryption Standard(AES),高级加密标准,是典型的块加密,被设计来取代 DES,由 Joan Daemen 和 Vincent Rijmen 所设计。其基本信息如下
- 输入:128 比特。
- 输出:128 比特。
- SPN 网络结构。
其迭代轮数与密钥长度有关系,如下
| 密钥长度(比特) | 迭代轮数 |
|---|---|
| 128 | 10 |
| 192 | 12 |
| 256 | 14 |
基本流程
基本概念
在 AES 加解密过程中,每一块都是 128 比特,所以我们这里明确一些基本概念。
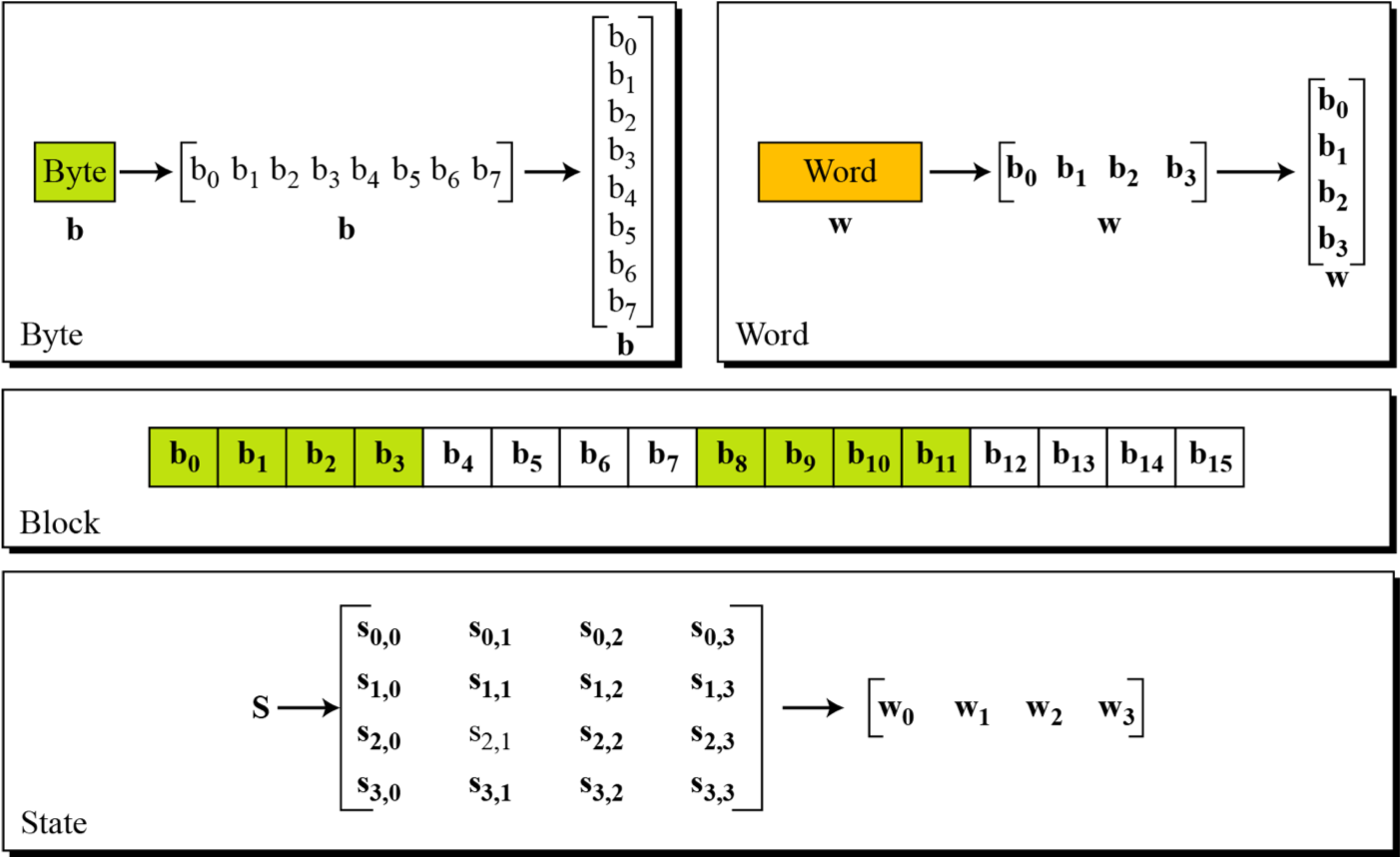
在 AES 中,块与 State 之间的转换过程如下
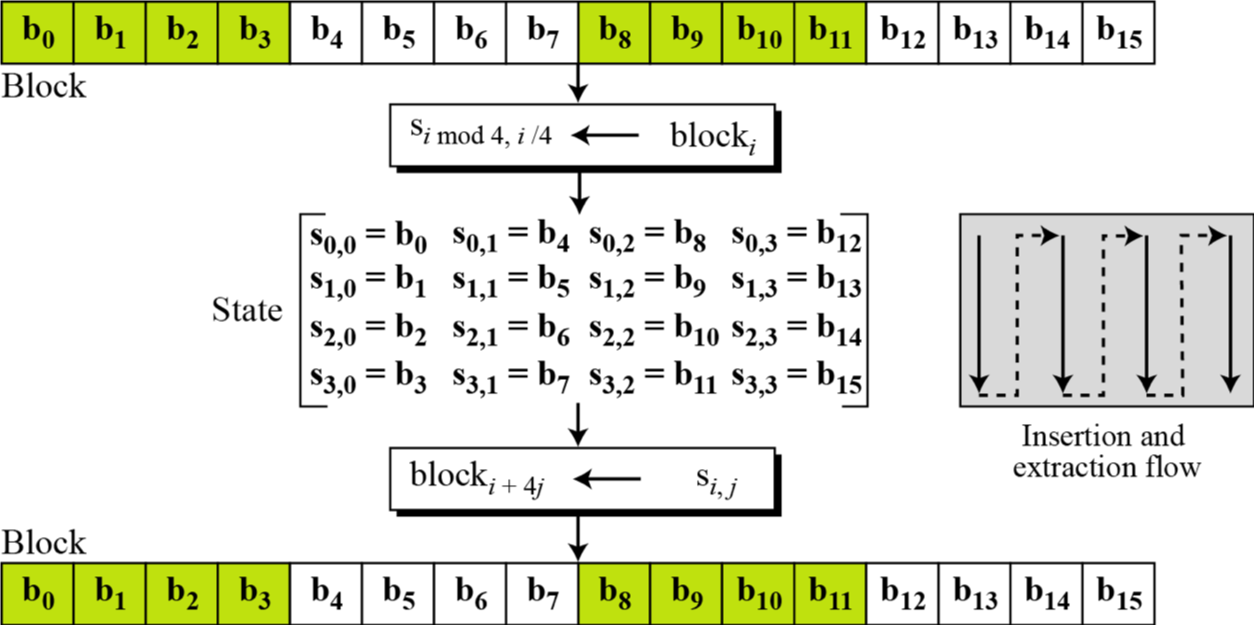
所以,可以看出,每一个 block 中的字节是按照列排列进入到状态数组的。
而对于明文来说,一般我们会选择使用其十六进制进行编码。
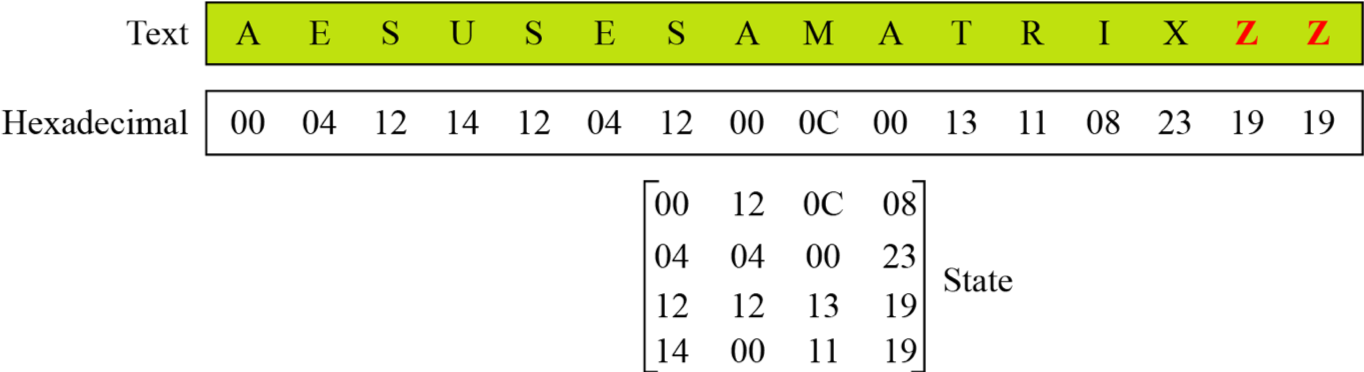
加解密过程
这里给个看雪上比较好的 图例 ,以便于介绍基本的流程,每一轮主要包括
- 轮密钥加,AddRoundKey
- 字节替换,SubBytes
- 行移位,ShiftRows
- 列混淆,MixColumns
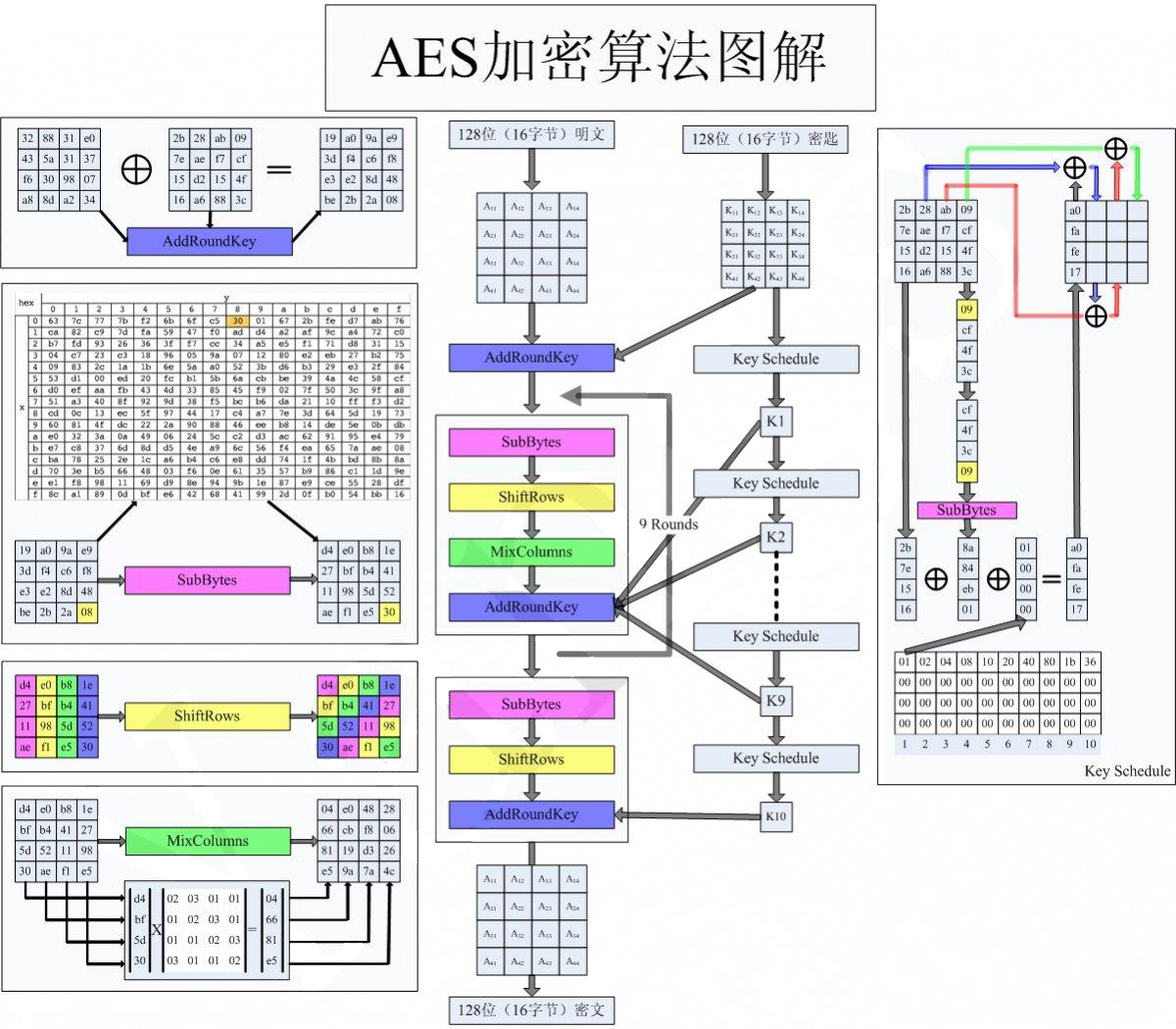
上面的列混淆的矩阵乘法等号左边的列向量应该在右边。
这里再给一张其加解密的全图,其解密算法的正确性很显然。
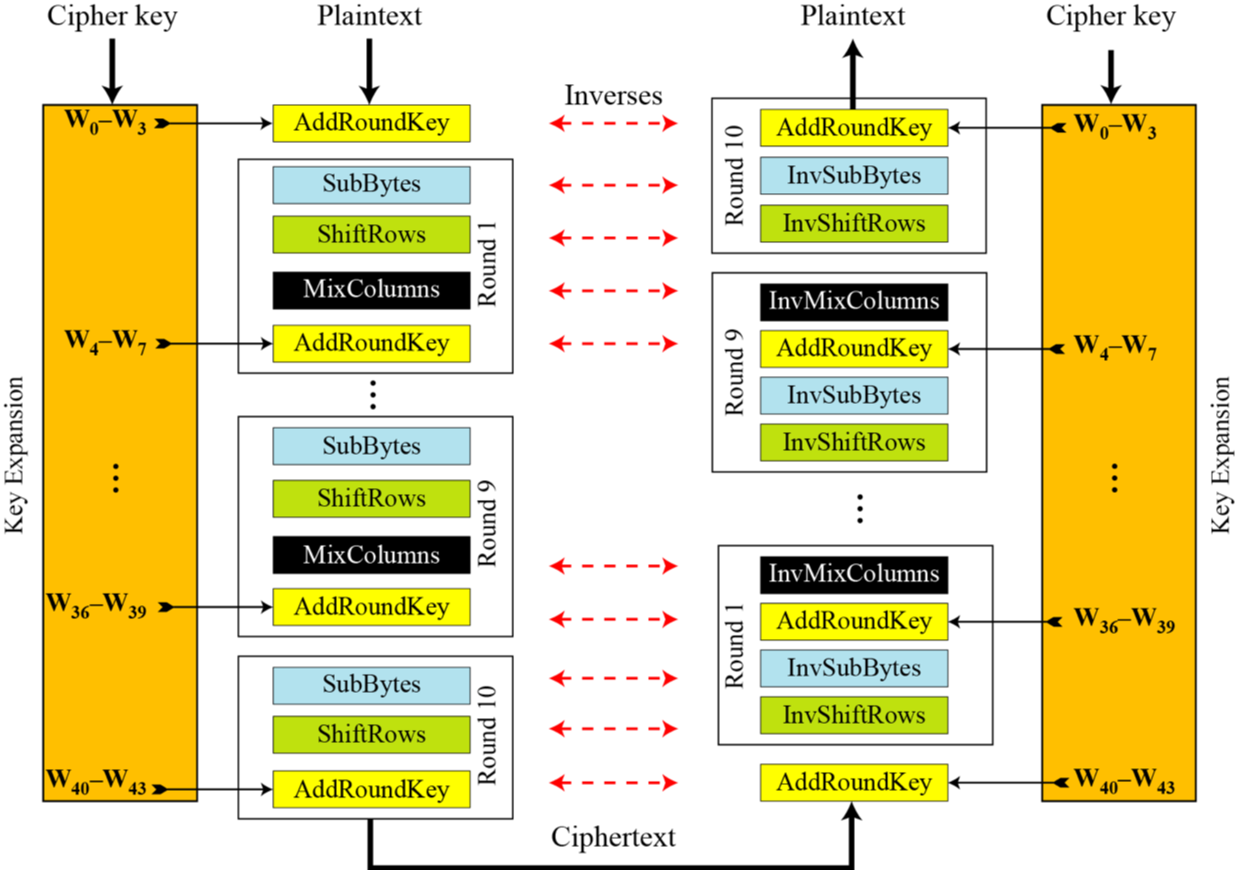
我们这里重点关注一下以下。
字节替换
在字节替换的背后,其实是有对应的数学规则来定义对应的替换表的,如下
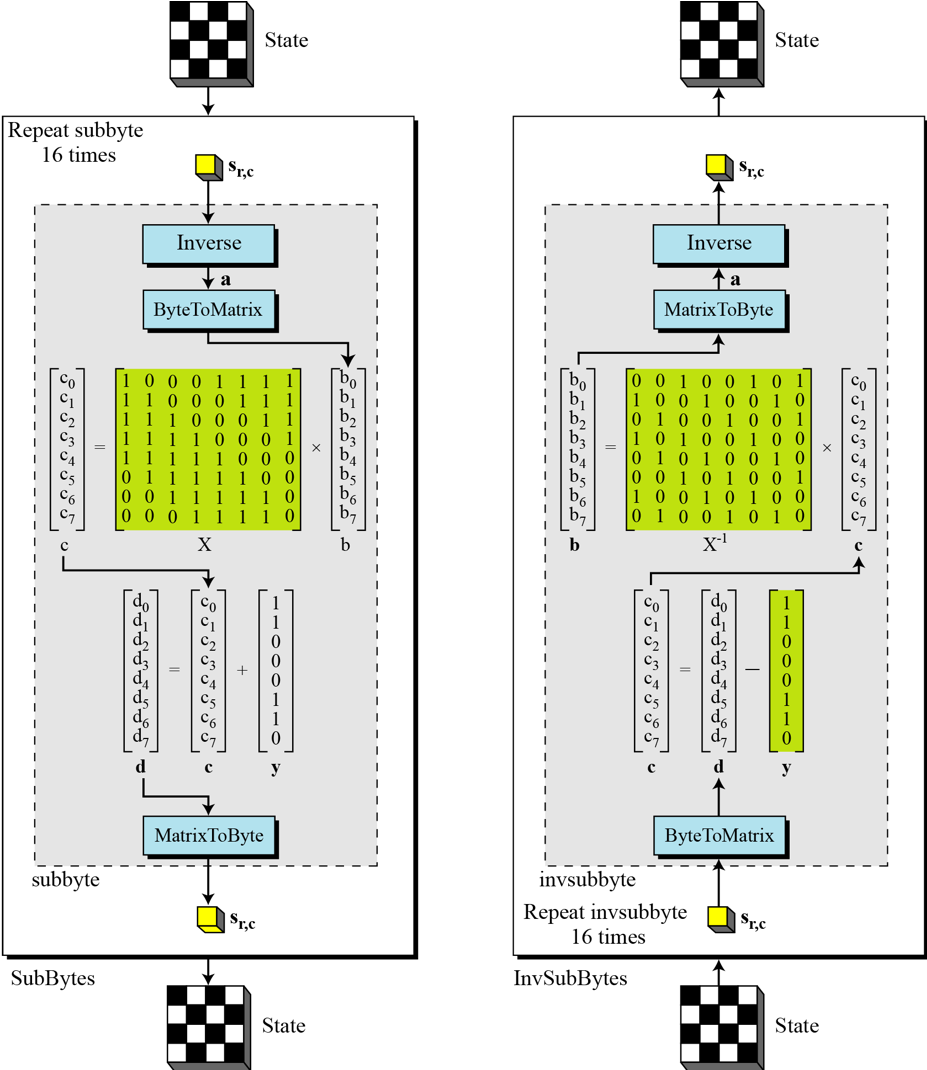
这里的运算均定义在 \(GF(2^8)\) 内。
列混淆
这里的运算也是定义在 \(GF(2^8)\) 上,使用的模多项式为 \(x^8+x^4+x^3+1\)。
密钥扩展
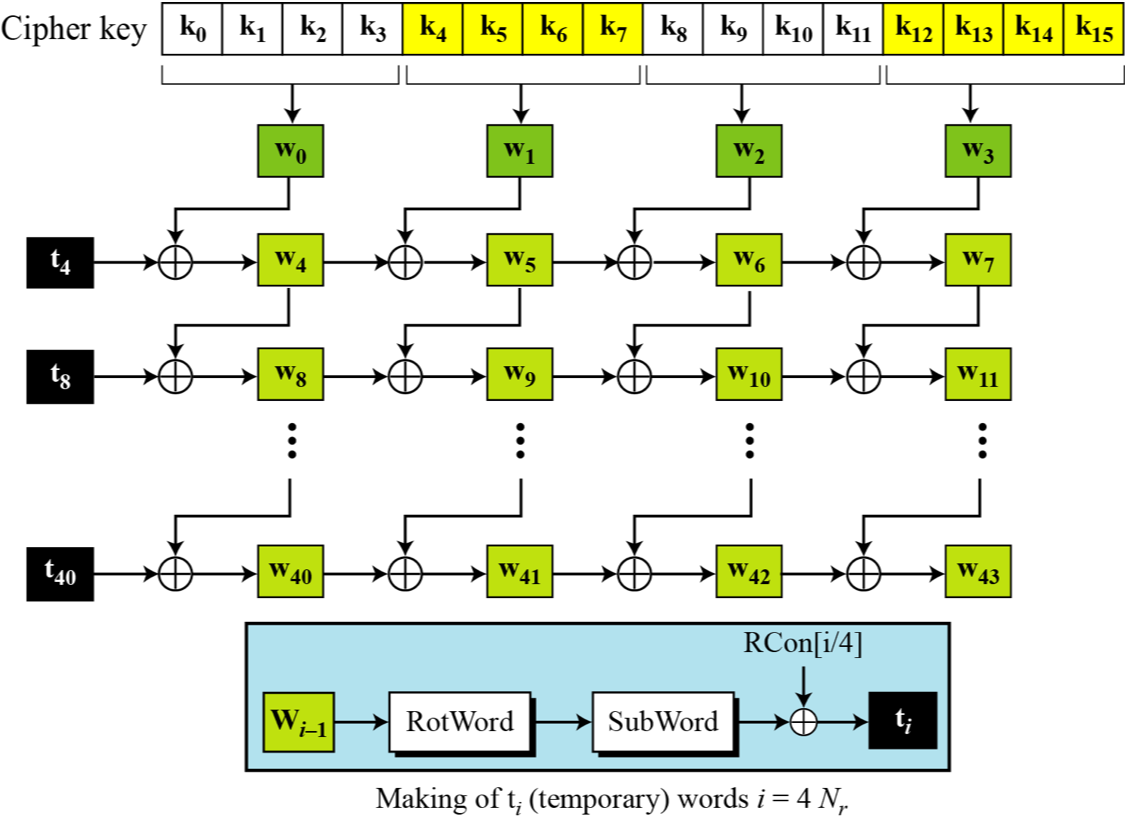
等价解密算法
简单分析一下,我们可以发现
- 交换逆向行移位和逆向字节代替并不影响结果。
- 交换轮密钥加和逆向列混淆并不影响结果,关键在于
- 首先可以把异或看成域上的多项式加法
- 然后多项式中乘法对加法具有分配率。
攻击方法
- 积分攻击
非对称加密
介绍
在非对称密码中,加密者与解密者所使用的密钥并不一样,典型的有 RSA 加密,背包加密,椭圆曲线加密。
RSA
RSA 加密算法是一种非对称加密算法。在公开密钥加密和电子商业中 RSA 被广泛使用。RSA 是 1977 年由罗纳德·李维斯特(Ron Rivest)、阿迪·萨莫尔(Adi Shamir)和伦纳德·阿德曼(Leonard Adleman)一起提出的。RSA 就是他们三人姓氏开头字母拼在一起组成的。
RSA 算法的可靠性由极大整数因数分解的难度决定。换言之,对一极大整数做因数分解愈困难,RSA 算法愈可靠。假如有人找到一种快速因数分解的算法的话,那么用 RSA 加密的信息的可靠性就肯定会极度下降。但找到这样的算法的可能性是非常小的。如今,只有短的 RSA 密钥才可能被强力方式解破。到 2020 年为止,还没有任何可靠的攻击 RSA 算法的方式。
基本原理
公钥与私钥的产生
- 随机选择两个不同大质数 \(p\) 和 \(q\),计算 \(N = p \times q\)
- 根据欧拉函数,求得 \(\varphi (N)=\varphi (p)\varphi (q)=(p-1)(q-1)\)
- 选择一个小于 \(\varphi (N)\) 的整数 \(e\),使 \(e\) 和 \(\varphi (N)\) 互质。并求得 \(e\) 关于 \(\varphi (N)\) 的模反元素,命名为 \(d\),有 \(ed\equiv 1 \pmod {\varphi (N)}\)
- 将 \(p\) 和 \(q\) 的记录销毁
此时,\((N,e)\) 是公钥,\((N,d)\) 是私钥。
消息加密
首先需要将消息 以一个双方约定好的格式转化为一个小于 \(N\),且与 \(N\) 互质的整数 \(m\)。如果消息太长,可以将消息分为几段,这也就是我们所说的块加密,后对于每一部分利用如下公式加密:
\[ m^{e}\equiv c\pmod N \]
消息解密
利用密钥 \(d\) 进行解密。
\[ c^{d}\equiv m\pmod N \]
正确性证明
即我们要证\(m^{ed} \equiv m \bmod N\),已知\(ed \equiv 1 \bmod \phi(N)\),那么 \(ed=k\phi(N)+1\),即需要证明
\[ m^{k\phi(N)+1} \equiv m \bmod N \]
这里我们分两种情况证明
第一种情况 \(gcd(m,N)=1\),那么 \(m^{\phi(N)} \equiv 1 \bmod N\),因此原式成立。
第二种情况 \(gcd(m,N)\neq 1\),那么 \(m\) 必然是 \(p\) 或者 \(q\) 的倍数,并且 \(n=m\) 小于 \(N\)。我们假设
\[ m=xp \]
那么 \(x\) 必然小于 \(q\),又由于 \(q\) 是素数。那么
\[ m^{\phi(q)} \equiv 1 \bmod q \]
进而
\[ m^{k\phi(N)}=m^{k(p-1)(q-1)}=(m^{\phi(q)})^{k(p-1)} \equiv 1 \bmod q \]
那么
\[ m^{k\phi(N)+1}=m+uqm \]
进而
\[ m^{k\phi(N)+1}=m+uqxp=m+uxN \]
所以原式成立。
样例
例1
计算公钥和私钥
p = 13 , q = 5
- N = pq = 65
- r = (p-1)(q-1) = (13-1)(5-1) = 48
计算模反元素 r=48,选择e=5,得到二元一次方程:5d-48k=1 , 获得一组解:d=29,k=3
因此,公钥是 (N, e) = (65, 5),私钥是 (N, d) = (65, 29)。
加密信息
明文:m=3
计算: $ c ^{5} $
因此:3被加密为48
解密信息
密文:c=48
计算:$ n ^{29} $
因此:48被解密为3
例2

密码协议
Diffie-Hellman 密钥交换
- 密钥交换是实现安全通信的基础
- 商用加密算法AES和DES需要在安全通信之前,实现通信双方的密钥共享。
- 密钥交换的方法:
- 基于RSA的密钥交换;
- 基于KDC技术 (Key Distributed Center,密钥分发中心);
- Diffie-Hellman密钥交换(简称:DH算法);
- 基于物理层的密钥交换。
DH算法是不安全信道下实现安全密钥共享的一种方法,由 W. Diffie 和 M.Hellman 在1976年提出的第一个公开的公钥密码算法。
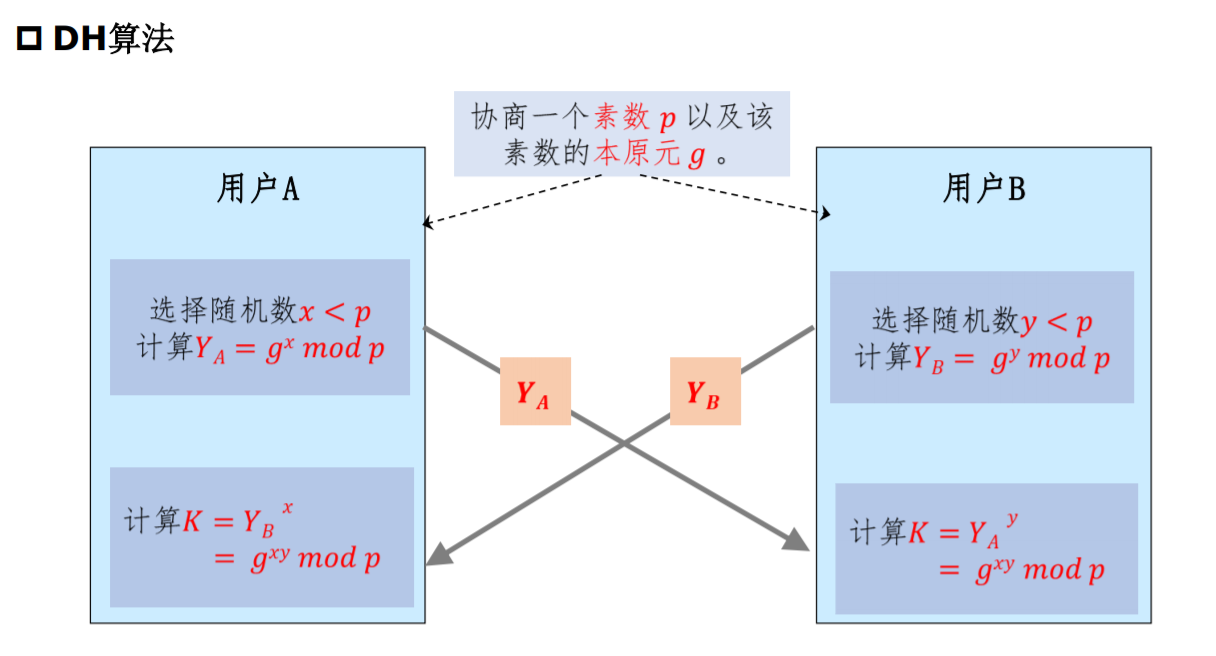
DH协议案例

